Machine Learning Library¶
MLlib is Spark’s machine learning (ML) library. Its goal is to make practical machine learning scalable and easy. At a high level, it provides tools such as:
- ML Algorithms: common learning algorithms such as classification, regression, clustering, and collaborative filtering
- Featurization: feature extraction, transformation, dimensionality reduction, and selection
- Pipelines: tools for constructing, evaluating, and tuning ML Pipelines
- Persistence: saving and load algorithms, models, and Pipelines
- Utilities: linear algebra, statistics, data handling, etc.
MLlib APIs¶
The RDD-based APIs in the
spark.mllibpackage have entered maintenance mode.The primary Machine Learning API for Spark is now the DataFrame-based API in the
spark.mlpackage.Why the DataFrame-based API?
DataFrames provide a more user-friendly API than RDDs. The many benefits of DataFrames include Spark Datasources, SQL/DataFrame queries, Tungsten and Catalyst optimizations, and uniform APIs across languages.
The DataFrame-based API for MLlib provides a uniform API across ML algorithms and across multiple languages.
DataFrames facilitate practical ML Pipelines, particularly feature transformations. See the Pipelines guide for details.
Start a Spark session¶
spark, sc = %spark.get_session ml
24/04/15 07:09:05 WARN [Thread-4] Client: Neither spark.yarn.jars nor spark.yarn.archive is set, falling back to uploading libraries under SPARK_HOME.
Correlation¶
Calculating the correlation between two series of data is a common operation in Statistics.
The
spark.mllibandspark.mlprovides the flexibility to calculate pairwise correlations among many series. The supported correlation methods are currently Pearson’s and Spearman’s correlation.
from pyspark.mllib.stat import Statistics
import numpy as np
seriesX = sc.parallelize([1.0, 2.0, 3.0, 3.0, 5.0]) # a series
# seriesY must have the same number of partitions and cardinality as seriesX
seriesY = sc.parallelize([11.0, 22.0, 33.0, 33.0, 555.0])
# Compute the correlation using Pearson's method. Enter "spearman" for Spearman's method.
# If a method is not specified, Pearson's method will be used by default.
print("Correlation is: " + str(Statistics.corr(seriesX, seriesY, method="pearson")))
data = sc.parallelize(
[np.array([1.0, 10.0, 100.0]), np.array([2.0, 20.0, 200.0]), np.array([5.0, 33.0, 366.0])]
) # an RDD of Vectors
# calculate the correlation matrix using Pearson's method. Use "spearman" for Spearman's method.
# If a method is not specified, Pearson's method will be used by default.
print(Statistics.corr(data, method="pearson"))
Correlation is: 0.8500286768773005
[[1. 0.97888347 0.99038957] [0.97888347 1. 0.99774832] [0.99038957 0.99774832 1. ]]
from pyspark.ml.linalg import Vectors
from pyspark.ml.stat import Correlation
data = [(Vectors.sparse(4, [(0, 1.0), (3, -2.0)]),),
(Vectors.dense([4.0, 5.0, 0.0, 3.0]),),
(Vectors.dense([6.0, 7.0, 0.0, 8.0]),),
(Vectors.sparse(4, [(0, 9.0), (3, 1.0)]),)]
df = spark.createDataFrame(data, ["features"])
r1 = Correlation.corr(df, "features").head()
print("Pearson correlation matrix:\n" + str(r1[0]))
r2 = Correlation.corr(df, "features", "spearman").head()
print("Spearman correlation matrix:\n" + str(r2[0]))
24/04/15 06:34:37 WARN [Thread-4] PearsonCorrelation: Pearson correlation matrix contains NaN values.
Pearson correlation matrix:
DenseMatrix([[1. , 0.05564149, nan, 0.40047142],
[0.05564149, 1. , nan, 0.91359586],
[ nan, nan, 1. , nan],
[0.40047142, 0.91359586, nan, 1. ]])
Spearman correlation matrix:
DenseMatrix([[1. , 0.10540926, nan, 0.4 ],
[0.10540926, 1. , nan, 0.9486833 ],
[ nan, nan, 1. , nan],
[0.4 , 0.9486833 , nan, 1. ]])
24/04/15 06:34:39 WARN [Thread-4] PearsonCorrelation: Pearson correlation matrix contains NaN values.
help(Vectors.sparse)
Help on function sparse in module pyspark.ml.linalg:
sparse(size: int, *args: Union[bytes, Tuple[int, float], Iterable[float], Iterable[Tuple[int, float]], Dict[int, float]]) -> pyspark.ml.linalg.SparseVector
Create a sparse vector, using either a dictionary, a list of
(index, value) pairs, or two separate arrays of indices and
values (sorted by index).
Parameters
----------
size : int
Size of the vector.
args
Non-zero entries, as a dictionary, list of tuples,
or two sorted lists containing indices and values.
Examples
--------
>>> Vectors.sparse(4, {1: 1.0, 3: 5.5})
SparseVector(4, {1: 1.0, 3: 5.5})
>>> Vectors.sparse(4, [(1, 1.0), (3, 5.5)])
SparseVector(4, {1: 1.0, 3: 5.5})
>>> Vectors.sparse(4, [1, 3], [1.0, 5.5])
SparseVector(4, {1: 1.0, 3: 5.5})
Note that you can refer to here for data types in mllib.
Summarizer¶
The
spark.mllibandspark.mlprovides vector column summary statistics for Dataframe through Summarizer.Available metrics are the column-wise
max,min,mean,variance, and number ofnonzeros, as well as the totalcount.
from pyspark.mllib.stat import Statistics
mat = sc.parallelize(
[np.array([1.0, 10.0, 100.0]), np.array([2.0, 20.0, 200.0]), np.array([3.0, 30.0, 300.0])]
) # an RDD of Vectors
# Compute column summary statistics.
summary = Statistics.colStats(mat)
print(summary.mean()) # a dense vector containing the mean value for each column
print(summary.variance()) # column-wise variance
print(summary.numNonzeros()) # number of nonzeros in each column
[ 2. 20. 200.] [1.e+00 1.e+02 1.e+04] [3. 3. 3.]
from pyspark.ml.stat import Summarizer
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
df = sc.parallelize([Row(weight=1.0, features=Vectors.dense(1.0, 1.0, 1.0)),
Row(weight=0.0, features=Vectors.dense(1.0, 2.0, 3.0))]).toDF()
# create summarizer for multiple metrics "mean" and "count"
summarizer = Summarizer.metrics("mean", "count")
# compute statistics for multiple metrics with weight
df.select(summarizer.summary(df.features, df.weight)).show(truncate=False)
# compute statistics for multiple metrics without weight
df.select(summarizer.summary(df.features)).show(truncate=False)
# compute statistics for single metric "mean" with weight
df.select(Summarizer.mean(df.features, df.weight)).show(truncate=False)
# compute statistics for single metric "mean" without weight
df.select(Summarizer.mean(df.features)).show(truncate=False)
+-----------------------------------+
|aggregate_metrics(features, weight)|
+-----------------------------------+
|{[1.0,1.0,1.0], 1} |
+-----------------------------------+
+--------------------------------+
|aggregate_metrics(features, 1.0)|
+--------------------------------+
|{[1.0,1.5,2.0], 2} |
+--------------------------------+
+--------------+
|mean(features)|
+--------------+
|[1.0,1.0,1.0] |
+--------------+
+--------------+
|mean(features)|
+--------------+
|[1.0,1.5,2.0] |
+--------------+
Testing¶
spark.mllibandspark.mlcurrently supports Pearson’s chi-squared ($\chi^2$) tests for goodness of fit and independence.Statisticsprovides methods to run a 1-sample, 2-sided Kolmogorov-Smirnov test.
from pyspark.mllib.linalg import Matrices, Vectors
from pyspark.mllib.regression import LabeledPoint
from pyspark.mllib.stat import Statistics
vec = Vectors.dense(0.1, 0.15, 0.2, 0.3, 0.25) # a vector composed of the frequencies of events
# compute the goodness of fit. If a second vector to test against
# is not supplied as a parameter, the test runs against a uniform distribution.
goodnessOfFitTestResult = Statistics.chiSqTest(vec)
# summary of the test including the p-value, degrees of freedom,
# test statistic, the method used, and the null hypothesis.
print("%s\n" % goodnessOfFitTestResult)
mat = Matrices.dense(3, 2, [1.0, 3.0, 5.0, 2.0, 4.0, 6.0]) # a contingency matrix
# conduct Pearson's independence test on the input contingency matrix
independenceTestResult = Statistics.chiSqTest(mat)
# summary of the test including the p-value, degrees of freedom,
# test statistic, the method used, and the null hypothesis.
print("%s\n" % independenceTestResult)
obs = sc.parallelize(
[LabeledPoint(1.0, [1.0, 0.0, 3.0]),
LabeledPoint(1.0, [1.0, 2.0, 0.0]),
LabeledPoint(1.0, [-1.0, 0.0, -0.5])]
) # LabeledPoint(label, feature)
# The contingency table is constructed from an RDD of LabeledPoint and used to conduct
# the independence test. Returns an array containing the ChiSquaredTestResult for every feature
# against the label.
featureTestResults = Statistics.chiSqTest(obs)
for i, result in enumerate(featureTestResults):
print("Column %d:\n%s" % (i + 1, result))
Chi squared test summary: method: pearson degrees of freedom = 4 statistic = 0.12499999999999999 pValue = 0.998126379239318 No presumption against null hypothesis: observed follows the same distribution as expected.. Chi squared test summary: method: pearson degrees of freedom = 2 statistic = 0.14141414141414144 pValue = 0.931734784568187 No presumption against null hypothesis: the occurrence of the outcomes is statistically independent.. Column 1: Chi squared test summary: method: pearson degrees of freedom = 0 statistic = 0.0 pValue = 1.0 No presumption against null hypothesis: the occurrence of the outcomes is statistically independent.. Column 2: Chi squared test summary: method: pearson degrees of freedom = 0 statistic = 0.0 pValue = 1.0 No presumption against null hypothesis: the occurrence of the outcomes is statistically independent.. Column 3: Chi squared test summary: method: pearson degrees of freedom = 0 statistic = 0.0 pValue = 1.0 No presumption against null hypothesis: the occurrence of the outcomes is statistically independent..
help(Statistics.chiSqTest)
Help on function chiSqTest in module pyspark.mllib.stat._statistics:
chiSqTest(observed: Union[pyspark.mllib.linalg.Matrix, pyspark.rdd.RDD[pyspark.mllib.regression.LabeledPoint], pyspark.mllib.linalg.Vector], expected: Optional[pyspark.mllib.linalg.Vector] = None) -> Union[pyspark.mllib.stat.test.ChiSqTestResult, List[pyspark.mllib.stat.test.ChiSqTestResult]]
If `observed` is Vector, conduct Pearson's chi-squared goodness
of fit test of the observed data against the expected distribution,
or against the uniform distribution (by default), with each category
having an expected frequency of `1 / len(observed)`.
If `observed` is matrix, conduct Pearson's independence test on the
input contingency matrix, which cannot contain negative entries or
columns or rows that sum up to 0.
If `observed` is an RDD of LabeledPoint, conduct Pearson's independence
test for every feature against the label across the input RDD.
For each feature, the (feature, label) pairs are converted into a
contingency matrix for which the chi-squared statistic is computed.
All label and feature values must be categorical.
Parameters
----------
observed : :py:class:`pyspark.mllib.linalg.Vector` or :py:class:`pyspark.mllib.linalg.Matrix`
it could be a vector containing the observed categorical
counts/relative frequencies, or the contingency matrix
(containing either counts or relative frequencies),
or an RDD of LabeledPoint containing the labeled dataset
with categorical features. Real-valued features will be
treated as categorical for each distinct value.
expected : :py:class:`pyspark.mllib.linalg.Vector`
Vector containing the expected categorical counts/relative
frequencies. `expected` is rescaled if the `expected` sum
differs from the `observed` sum.
Returns
-------
:py:class:`pyspark.mllib.stat.ChiSqTestResult`
object containing the test statistic, degrees
of freedom, p-value, the method used, and the null hypothesis.
Notes
-----
`observed` cannot contain negative values
Examples
--------
>>> from pyspark.mllib.linalg import Vectors, Matrices
>>> observed = Vectors.dense([4, 6, 5])
>>> pearson = Statistics.chiSqTest(observed)
>>> print(pearson.statistic)
0.4
>>> pearson.degreesOfFreedom
2
>>> print(round(pearson.pValue, 4))
0.8187
>>> pearson.method
'pearson'
>>> pearson.nullHypothesis
'observed follows the same distribution as expected.'
>>> observed = Vectors.dense([21, 38, 43, 80])
>>> expected = Vectors.dense([3, 5, 7, 20])
>>> pearson = Statistics.chiSqTest(observed, expected)
>>> print(round(pearson.pValue, 4))
0.0027
>>> data = [40.0, 24.0, 29.0, 56.0, 32.0, 42.0, 31.0, 10.0, 0.0, 30.0, 15.0, 12.0]
>>> chi = Statistics.chiSqTest(Matrices.dense(3, 4, data))
>>> print(round(chi.statistic, 4))
21.9958
>>> data = [LabeledPoint(0.0, Vectors.dense([0.5, 10.0])),
... LabeledPoint(0.0, Vectors.dense([1.5, 20.0])),
... LabeledPoint(1.0, Vectors.dense([1.5, 30.0])),
... LabeledPoint(0.0, Vectors.dense([3.5, 30.0])),
... LabeledPoint(0.0, Vectors.dense([3.5, 40.0])),
... LabeledPoint(1.0, Vectors.dense([3.5, 40.0])),]
>>> rdd = sc.parallelize(data, 4)
>>> chi = Statistics.chiSqTest(rdd)
>>> print(chi[0].statistic)
0.75
>>> print(chi[1].statistic)
1.5
from pyspark.ml.linalg import Vectors
from pyspark.ml.stat import ChiSquareTest
data = [(0.0, Vectors.dense(0.5, 10.0)),
(0.0, Vectors.dense(1.5, 20.0)),
(1.0, Vectors.dense(1.5, 30.0)),
(0.0, Vectors.dense(3.5, 30.0)),
(0.0, Vectors.dense(3.5, 40.0)),
(1.0, Vectors.dense(3.5, 40.0))]
df = spark.createDataFrame(data, ["label", "features"])
r = ChiSquareTest.test(df, "features", "label").head()
print("pValues: " + str(r.pValues))
print("degreesOfFreedom: " + str(r.degreesOfFreedom))
print("statistics: " + str(r.statistics))
pValues: [0.6872892787909721,0.6822703303362126] degreesOfFreedom: [2, 3] statistics: [0.75,1.5]
from pyspark.mllib.stat import Statistics
parallelData = sc.parallelize([0.1, 0.15, 0.2, 0.3, 0.25])
# run a KS test for the sample versus a standard normal distribution
testResult = Statistics.kolmogorovSmirnovTest(parallelData, "norm", 0, 1)
# summary of the test including the p-value, test statistic, and null hypothesis
# if our p-value indicates significance, we can reject the null hypothesis
# Note that the Scala functionality of calling Statistics.kolmogorovSmirnovTest with
# a lambda to calculate the CDF is not made available in the Python API
print(testResult)
Kolmogorov-Smirnov test summary: degrees of freedom = 0 statistic = 0.539827837277029 pValue = 0.06821463111921133 Low presumption against null hypothesis: Sample follows theoretical distribution.
Random number generation¶
RandomRDDsprovides factory methods to generate random double RDDs or vector RDDs. The following example generates a random double RDD, whose values follows the standard normal distribution $N(0, 1)$, and then map it to $N(1, 4)$.
from pyspark.mllib.random import RandomRDDs
# Generate a random double RDD that contains 1 million i.i.d. values drawn from the
# standard normal distribution `N(0, 1)`, evenly distributed in 10 partitions.
u = RandomRDDs.normalRDD(sc, 1000000, 10)
# Apply a transform to get a random double RDD following `N(1, 4)`.
v = u.map(lambda x: 1.0 + 2.0 * x)
Kernel density estimation¶
- Kernel density estimation is a technique useful for visualizing empirical probability distributions without requiring assumptions about the particular distribution that the observed samples are drawn from.
from pyspark.mllib.stat import KernelDensity
# an RDD of sample data
data = sc.parallelize([1.0, 1.0, 1.0, 2.0, 3.0, 4.0, 5.0, 5.0, 6.0, 7.0, 8.0, 9.0, 9.0])
# Construct the density estimator with the sample data and a standard deviation for the Gaussian
# kernels
kd = KernelDensity()
kd.setSample(data)
kd.setBandwidth(3.0)
# Find density estimates for the given values
densities = kd.estimate([-1.0, 2.0, 5.0])
densities
array([0.04145944, 0.07902017, 0.0896292 ])
Data sources¶
Besides some general data sources such as Parquet, CSV, JSON and JDBC, spark also supports some specific data sources for ML.
- Image data source.
- LIBSVM data source.
Image data source¶
This image data source is used to load image files from a directory, it can load compressed image (jpeg, png, etc.) into raw image representation via ImageIO in Java library. The loaded DataFrame has one StructType column: “image”, containing image data stored as image schema. The schema of the image column is:
- origin: StringType (represents the file path of the image)
- height: IntegerType (height of the image)
- width: IntegerType (width of the image)
- nChannels: IntegerType (number of image channels)
- mode: IntegerType (OpenCV-compatible type)
- data: BinaryType (Image bytes in OpenCV-compatible order: row-wise BGR in most cases)
import os
spark_home = os.getenv('SPARK_HOME')
df = spark.read.format("image").option("dropInvalid", True).load(f"file://{spark_home}/data/mllib/images/origin/kittens")
df.select("image.origin", "image.width", "image.height").show(truncate=False)
+-----------------------------------------------------------------------------------------------+-----+------+ |origin |width|height| +-----------------------------------------------------------------------------------------------+-----+------+ |file:///opt/apps/SPARK3/spark3-current/data/mllib/images/origin/kittens/54893.jpg |300 |311 | |file:///opt/apps/SPARK3/spark3-current/data/mllib/images/origin/kittens/DP802813.jpg |199 |313 | |file:///opt/apps/SPARK3/spark3-current/data/mllib/images/origin/kittens/29.5.a_b_EGDP022204.jpg|300 |200 | |file:///opt/apps/SPARK3/spark3-current/data/mllib/images/origin/kittens/DP153539.jpg |300 |296 | +-----------------------------------------------------------------------------------------------+-----+------+
LIBSVM data source¶
This LIBSVM data source is used to load ‘libsvm’ type files from a directory. The loaded DataFrame has two columns: label containing labels stored as doubles and features containing feature vectors stored as Vectors. The schemas of the columns are:
- label: DoubleType (represents the instance label).
- features: VectorUDT (represents the feature vector).
df = spark.read.format("libsvm").option("numFeatures", "780").load(f"file://{spark_home}/data/mllib/sample_libsvm_data.txt")
df.show(10)
+-----+--------------------+ |label| features| +-----+--------------------+ | 0.0|(780,[127,128,129...| | 1.0|(780,[158,159,160...| | 1.0|(780,[124,125,126...| | 1.0|(780,[152,153,154...| | 1.0|(780,[151,152,153...| | 0.0|(780,[129,130,131...| | 1.0|(780,[158,159,160...| | 1.0|(780,[99,100,101,...| | 0.0|(780,[154,155,156...| | 0.0|(780,[127,128,129...| +-----+--------------------+ only showing top 10 rows
Machine Learning Pipelines¶
MLlib standardizes APIs for machine learning algorithms to make it easier to combine multiple algorithms into a single pipeline, or workflow.
The pipeline concept is mostly inspired by the
scikit-learnproject.DataFrame: This ML API uses DataFrame from Spark SQL as an ML dataset, which can hold a variety of data types. E.g., a DataFrame could have different columns storing text, feature vectors, true labels, and predictions.Transformer: A Transformer is an algorithm which can transform one DataFrame into another DataFrame. E.g., an ML model is a Transformer which transforms a DataFrame with features into a DataFrame with predictions.Estimator: An Estimator is an algorithm which can be fit on a DataFrame to produce a Transformer. E.g., a learning algorithm is an Estimator which trains on a DataFrame and produces a model.Pipeline: A Pipeline chains multiple Transformers and Estimators together to specify an ML workflow.Parameter: All Transformers and Estimators now share a common API for specifying parameters.
DataFrame¶
Machine learning can be applied to a wide variety of data types, such as vectors, text, images, and structured data. This API adopts the
DataFramefrom Spark SQL in order to support a variety of data types.DataFramesupports many basic and structured types; see the Spark SQL datatype reference for a list of supported types. In addition to the types listed in the Spark SQL guide, DataFrame can use ML Vector types.A
DataFramecan be created either implicitly or explicitly from a regular RDD. See the code examples below and the Spark SQL programming guide for examples.Columns in a DataFrame are named. The code examples below use names such as “text”, “features”, and “label”.
Transformers¶
A Transformer is an abstraction that includes feature transformers and learned models. Technically, a Transformer implements a method transform(), which converts one DataFrame into another, generally by appending one or more columns. For example:
A feature transformer might take a DataFrame, read a column (e.g., text), map it into a new column (e.g., feature vectors), and output a new DataFrame with the mapped column appended.
A learning model might take a DataFrame, read the column containing feature vectors, predict the label for each feature vector, and output a new DataFrame with predicted labels appended as a column.
Estimators¶
An Estimator abstracts the concept of a learning algorithm or any algorithm that fits or trains on data. Technically, an Estimator implements a method fit(), which accepts a DataFrame and produces a Model, which is a Transformer. For example, a learning algorithm such as LogisticRegression is an Estimator, and calling fit() trains a LogisticRegressionModel, which is a Model and hence a Transformer.
Properties of pipeline components¶
Transformer.transform()sandEstimator.fit()sare both stateless. In the future, stateful algorithms may be supported via alternative concepts.Each instance of a
TransformerorEstimatorhas a unique ID, which is useful in specifying parameters (discussed below).
Pipeline¶
In machine learning, it is common to run a sequence of algorithms to process and learn from data. E.g., a simple text document processing workflow might include several stages:
- Split each document’s text into words.
- Convert each document’s words into a numerical feature vector.
- Learn a prediction model using the feature vectors and labels.
MLlib represents such a workflow as a Pipeline, which consists of a sequence of PipelineStages (Transformers and Estimators) to be run in a specific order. We will use this simple workflow as a running example in this section.
How it works?¶
- A Pipeline is specified as a sequence of stages, and each stage is either a Transformer or an Estimator.
- These stages are run in order, and the input DataFrame is transformed as it passes through each stage.
- For Transformer stages, the transform() method is called on the DataFrame.
- For Estimator stages, the fit() method is called to produce a Transformer (which becomes part of the PipelineModel, or fitted Pipeline), and that Transformer’s transform() method is called on the DataFrame.
We illustrate this for the simple text document workflow. The figure below is for the training time usage of a Pipeline.
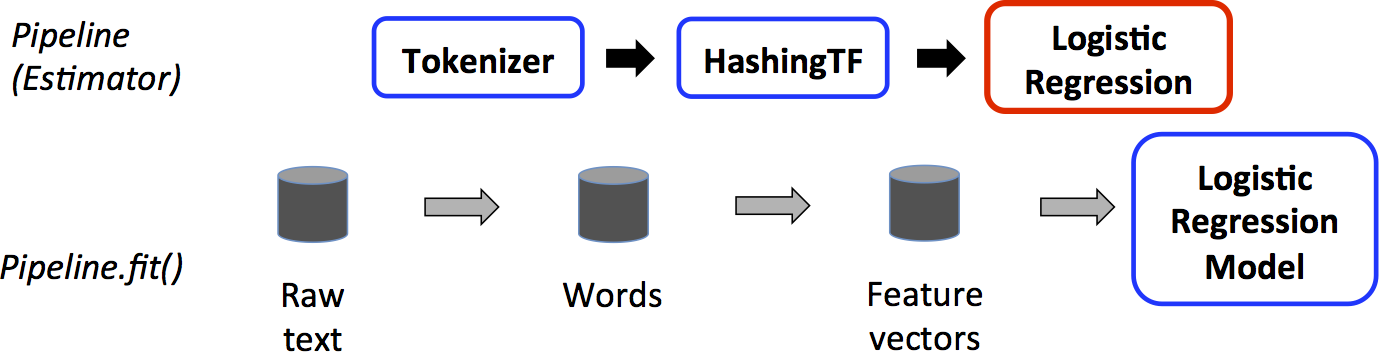
This PipelineModel is used at test time; the figure below illustrates this usage.
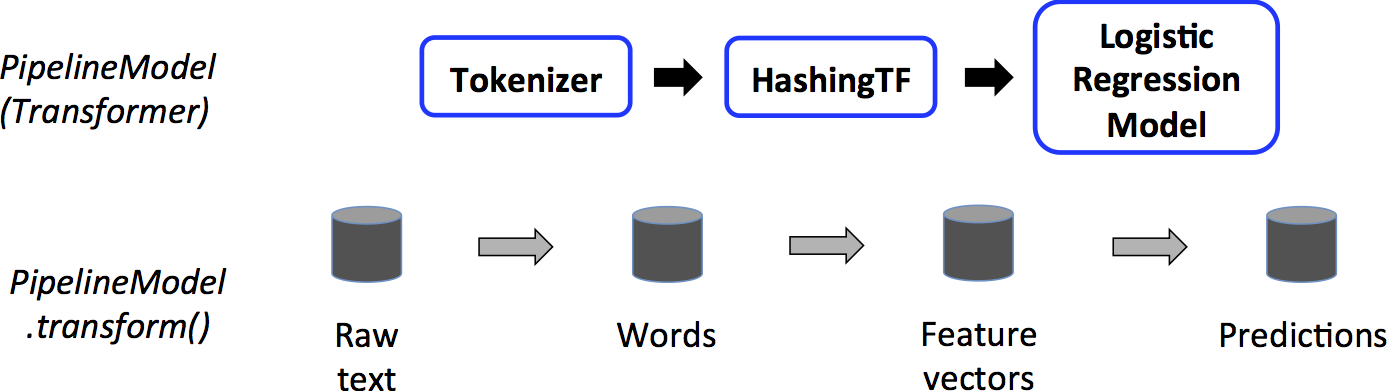
Pipline example: Linear Regression¶
df=spark.read.options(header='true', inferSchema='true').csv("/data/cruise_ship_info.csv")
df.show(10)
[Stage 2:> (0 + 1) / 1]
+-----------+-----------+---+------------------+----------+------+------+-----------------+----+ | Ship_name|Cruise_line|Age| Tonnage|passengers|length|cabins|passenger_density|crew| +-----------+-----------+---+------------------+----------+------+------+-----------------+----+ | Journey| Azamara| 6|30.276999999999997| 6.94| 5.94| 3.55| 42.64|3.55| | Quest| Azamara| 6|30.276999999999997| 6.94| 5.94| 3.55| 42.64|3.55| |Celebration| Carnival| 26| 47.262| 14.86| 7.22| 7.43| 31.8| 6.7| | Conquest| Carnival| 11| 110.0| 29.74| 9.53| 14.88| 36.99|19.1| | Destiny| Carnival| 17| 101.353| 26.42| 8.92| 13.21| 38.36|10.0| | Ecstasy| Carnival| 22| 70.367| 20.52| 8.55| 10.2| 34.29| 9.2| | Elation| Carnival| 15| 70.367| 20.52| 8.55| 10.2| 34.29| 9.2| | Fantasy| Carnival| 23| 70.367| 20.56| 8.55| 10.22| 34.23| 9.2| |Fascination| Carnival| 19| 70.367| 20.52| 8.55| 10.2| 34.29| 9.2| | Freedom| Carnival| 6|110.23899999999999| 37.0| 9.51| 14.87| 29.79|11.5| +-----------+-----------+---+------------------+----------+------+------+-----------------+----+ only showing top 10 rows
#prints structure of dataframe along with datatype
df.printSchema()
root |-- Ship_name: string (nullable = true) |-- Cruise_line: string (nullable = true) |-- Age: integer (nullable = true) |-- Tonnage: double (nullable = true) |-- passengers: double (nullable = true) |-- length: double (nullable = true) |-- cabins: double (nullable = true) |-- passenger_density: double (nullable = true) |-- crew: double (nullable = true)
#In our predictive model, below are the columns
df.columns
['Ship_name', 'Cruise_line', 'Age', 'Tonnage', 'passengers', 'length', 'cabins', 'passenger_density', 'crew']
#columns identified as features are as below:
#['Cruise_line','Age','Tonnage','passengers','length','cabins','passenger_density']
#to work on the features, spark MLlib expects every value to be in numeric form
#feature 'Cruise_line is string datatype
#using StringIndexer, string type will be typecast to numeric datatype
#import library strinindexer for typecasting
from pyspark.ml.feature import StringIndexer
indexer=StringIndexer(inputCol='Cruise_line',outputCol='cruise_cat')
indexed=indexer.fit(df).transform(df)
#above code will convert string to numeric feature and create a new dataframe
#new dataframe contains a new feature 'cruise_cat' and can be used further
#feature cruise_cat is now vectorized and can be used to fed to model
for item in indexed.head(5):
print(item)
print('\n')
Row(Ship_name='Journey', Cruise_line='Azamara', Age=6, Tonnage=30.276999999999997, passengers=6.94, length=5.94, cabins=3.55, passenger_density=42.64, crew=3.55, cruise_cat=16.0) Row(Ship_name='Quest', Cruise_line='Azamara', Age=6, Tonnage=30.276999999999997, passengers=6.94, length=5.94, cabins=3.55, passenger_density=42.64, crew=3.55, cruise_cat=16.0) Row(Ship_name='Celebration', Cruise_line='Carnival', Age=26, Tonnage=47.262, passengers=14.86, length=7.22, cabins=7.43, passenger_density=31.8, crew=6.7, cruise_cat=1.0) Row(Ship_name='Conquest', Cruise_line='Carnival', Age=11, Tonnage=110.0, passengers=29.74, length=9.53, cabins=14.88, passenger_density=36.99, crew=19.1, cruise_cat=1.0) Row(Ship_name='Destiny', Cruise_line='Carnival', Age=17, Tonnage=101.353, passengers=26.42, length=8.92, cabins=13.21, passenger_density=38.36, crew=10.0, cruise_cat=1.0)
from pyspark.ml.linalg import Vectors
from pyspark.ml.feature import VectorAssembler
#creating vectors from features
#Apache MLlib takes input if vector form
assembler=VectorAssembler(inputCols=['Age',
'Tonnage',
'passengers',
'length',
'cabins',
'passenger_density',
'cruise_cat'],outputCol='features')
output=assembler.transform(indexed)
output.select('features','crew').show(5)
+--------------------+----+ | features|crew| +--------------------+----+ |[6.0,30.276999999...|3.55| |[6.0,30.276999999...|3.55| |[26.0,47.262,14.8...| 6.7| |[11.0,110.0,29.74...|19.1| |[17.0,101.353,26....|10.0| +--------------------+----+ only showing top 5 rows
#final data consist of features and label which is crew.
final_data=output.select('features','crew')
#splitting data into train and test
train_data,test_data=final_data.randomSplit([0.7,0.3])
train_data.describe().show()
+-------+-----------------+ |summary| crew| +-------+-----------------+ | count| 111| | mean|7.340990990990999| | stddev|3.288713745511779| | min| 0.6| | max| 13.6| +-------+-----------------+
#import LinearRegression library
from pyspark.ml.regression import LinearRegression
#creating an object of class LinearRegression
#object takes features and label as input arguments
ship_lr=LinearRegression(featuresCol='features',labelCol='crew')
#pass train_data to train model
trained_ship_model=ship_lr.fit(train_data)
#evaluating model trained for Rsquared error
ship_results=trained_ship_model.evaluate(train_data)
print('Rsquared:',ship_results.r2)
#R2 value shows accuracy of model is 92%
#model accuracy is very good and can be use for predictive analysis
24/04/15 07:13:54 WARN [Thread-4] Instrumentation: [2af668f9] regParam is zero, which might cause numerical instability and overfitting.
Rsquared: 0.9434156654009597
#testing Model on unlabeled data
#create unlabeled data from test_data
#testing model on unlabeled data
unlabeled_data=test_data.select('features')
unlabeled_data.show(5)
predictions=trained_ship_model.transform(unlabeled_data)
predictions.show()
+--------------------+ | features| +--------------------+ |[4.0,220.0,54.0,1...| |[5.0,86.0,21.04,9...| |[5.0,115.0,35.74,...| |[5.0,160.0,36.34,...| |[6.0,90.0,20.0,9....| +--------------------+ only showing top 5 rows +--------------------+------------------+ | features| prediction| +--------------------+------------------+ |[4.0,220.0,54.0,1...|20.478712471022856| |[5.0,86.0,21.04,9...| 9.41210066138852| |[5.0,115.0,35.74,...|11.517004449474037| |[5.0,160.0,36.34,...|15.090679542900594| |[6.0,90.0,20.0,9....|10.226391034054009| |[6.0,158.0,43.7,1...|13.737211922076828| |[7.0,116.0,31.0,9...|12.486491051271393| |[8.0,91.0,22.44,9...|10.210821356265736| |[9.0,81.0,21.44,9...| 9.60355235433488| |[9.0,105.0,27.2,8...|11.135795349583761| |[9.0,110.0,29.74,...|11.979908446474163| |[10.0,46.0,7.0,6....| 2.953210370822041| |[10.0,68.0,10.8,7...|6.6294896955530165| |[10.0,81.76899999...| 9.010646639419164| |[10.0,91.62700000...| 9.411354564281664| |[10.0,138.0,31.14...|12.983115659844682| |[11.0,90.0,22.4,9...|10.143640750324483| |[11.0,91.62700000...| 9.396040219356987| |[11.0,110.0,29.74...| 11.9626483194532| |[12.0,77.104,20.0...| 8.803272077595475| +--------------------+------------------+ only showing top 20 rows
Apache Spark's MLlib supports both Lasso and Ridge regression through the LinearRegression class by setting the elasticNetParam. The elasticNetParam is used to balance between Lasso and Ridge regression. A value of 0.0 means the penalty is an L2 penalty (Ridge regression), 1.0 means it is an L1 penalty (Lasso regression), and anything in between specifies the ratio of L1 to L2 penalty (Elastic Net).
Mathematical formulation¶
Many standard machine learning methods can be formulated as a convex optimization problem, i.e. the task of finding a minimizer of a convex function $f$ that depends on a variable vector $w$ (called weights in the code), which has $d$entries. Formally, we can write this as the optimization problem $\min f(w)$, where the objective function is of the form $f(w) := \lambda R(w) + \frac1 n \sum_{i=1}^n L(w;x_i,y_i)$.
Implementation idea of LinearRegression (using gradient descent)¶
- Distribute the Dataset.
- Local Gradient Calculation: Each node computes the gradient based on its local data partition. This step involves calculating the derivative of the loss function with respect to the model parameters for the subset of the data on that node. The local computation ensures that the workload is spread across the cluster, allowing for scalability and faster computation.
- Aggregate Gradients: After each node has computed its local gradient, these gradients need to be aggregated to update the model parameters globally. This aggregation can be done through techniques such as:
- Reduce Operation: A common approach where all local gradients are sent to a central node (e.g., the driver in Spark), summed, and then used to update the global model parameters.
- All-reduce Operation: An optimized version of reduce that aggregates gradients across nodes and then broadcasts the updated global model parameters back to all nodes, often more efficient and scalable.
- Update Global Model Parameters: Once the global gradient has been computed (i.e., the sum of all local gradients), it is used to update the model parameters. This step typically involves moving the parameters in the opposite direction of the gradient by a step size determined by the learning rate.
- Iterate Until Convergence.
- Convergence and Final Model.
Pipline example: Logistic Regression¶
from pyspark.ml.linalg import Vectors
from pyspark.ml.classification import LogisticRegression
# Prepare training data from a list of (label, features) tuples.
training = spark.createDataFrame([
(1.0, Vectors.dense([0.0, 1.1, 0.1])),
(0.0, Vectors.dense([2.0, 1.0, -1.0])),
(0.0, Vectors.dense([2.0, 1.3, 1.0])),
(1.0, Vectors.dense([0.0, 1.2, -0.5]))], ["label", "features"])
# Prepare test data
test = spark.createDataFrame([
(1.0, Vectors.dense([-1.0, 1.5, 1.3])),
(0.0, Vectors.dense([3.0, 2.0, -0.1])),
(1.0, Vectors.dense([0.0, 2.2, -1.5]))], ["label", "features"])
# Create a LogisticRegression instance. This instance is an Estimator.
lr = LogisticRegression(maxIter=10, regParam=0.01)
# Print out the parameters, documentation, and any default values.
print("LogisticRegression parameters:\n" + lr.explainParams() + "\n")
LogisticRegression parameters: aggregationDepth: suggested depth for treeAggregate (>= 2). (default: 2) elasticNetParam: the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty. (default: 0.0) family: The name of family which is a description of the label distribution to be used in the model. Supported options: auto, binomial, multinomial (default: auto) featuresCol: features column name. (default: features) fitIntercept: whether to fit an intercept term. (default: True) labelCol: label column name. (default: label) lowerBoundsOnCoefficients: The lower bounds on coefficients if fitting under bound constrained optimization. The bound matrix must be compatible with the shape (1, number of features) for binomial regression, or (number of classes, number of features) for multinomial regression. (undefined) lowerBoundsOnIntercepts: The lower bounds on intercepts if fitting under bound constrained optimization. The bounds vector size must beequal with 1 for binomial regression, or the number oflasses for multinomial regression. (undefined) maxBlockSizeInMB: maximum memory in MB for stacking input data into blocks. Data is stacked within partitions. If more than remaining data size in a partition then it is adjusted to the data size. Default 0.0 represents choosing optimal value, depends on specific algorithm. Must be >= 0. (default: 0.0) maxIter: max number of iterations (>= 0). (default: 100, current: 10) predictionCol: prediction column name. (default: prediction) probabilityCol: Column name for predicted class conditional probabilities. Note: Not all models output well-calibrated probability estimates! These probabilities should be treated as confidences, not precise probabilities. (default: probability) rawPredictionCol: raw prediction (a.k.a. confidence) column name. (default: rawPrediction) regParam: regularization parameter (>= 0). (default: 0.0, current: 0.01) standardization: whether to standardize the training features before fitting the model. (default: True) threshold: Threshold in binary classification prediction, in range [0, 1]. If threshold and thresholds are both set, they must match.e.g. if threshold is p, then thresholds must be equal to [1-p, p]. (default: 0.5) thresholds: Thresholds in multi-class classification to adjust the probability of predicting each class. Array must have length equal to the number of classes, with values > 0, excepting that at most one value may be 0. The class with largest value p/t is predicted, where p is the original probability of that class and t is the class's threshold. (undefined) tol: the convergence tolerance for iterative algorithms (>= 0). (default: 1e-06) upperBoundsOnCoefficients: The upper bounds on coefficients if fitting under bound constrained optimization. The bound matrix must be compatible with the shape (1, number of features) for binomial regression, or (number of classes, number of features) for multinomial regression. (undefined) upperBoundsOnIntercepts: The upper bounds on intercepts if fitting under bound constrained optimization. The bound vector size must be equal with 1 for binomial regression, or the number of classes for multinomial regression. (undefined) weightCol: weight column name. If this is not set or empty, we treat all instance weights as 1.0. (undefined)
# Learn a LogisticRegression model. This uses the parameters stored in lr.
model1 = lr.fit(training)
# Since model1 is a Model (i.e., a transformer produced by an Estimator),
# we can view the parameters it used during fit().
# This prints the parameter (name: value) pairs, where names are unique IDs for this
# LogisticRegression instance.
print("Model 1 was fit using parameters: ")
print(model1.extractParamMap())
Model 1 was fit using parameters:
{Param(parent='LogisticRegression_ce71e8a53e40', name='aggregationDepth', doc='suggested depth for treeAggregate (>= 2).'): 2, Param(parent='LogisticRegression_ce71e8a53e40', name='elasticNetParam', doc='the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty.'): 0.0, Param(parent='LogisticRegression_ce71e8a53e40', name='family', doc='The name of family which is a description of the label distribution to be used in the model. Supported options: auto, binomial, multinomial'): 'auto', Param(parent='LogisticRegression_ce71e8a53e40', name='featuresCol', doc='features column name.'): 'features', Param(parent='LogisticRegression_ce71e8a53e40', name='fitIntercept', doc='whether to fit an intercept term.'): True, Param(parent='LogisticRegression_ce71e8a53e40', name='labelCol', doc='label column name.'): 'label', Param(parent='LogisticRegression_ce71e8a53e40', name='maxBlockSizeInMB', doc='maximum memory in MB for stacking input data into blocks. Data is stacked within partitions. If more than remaining data size in a partition then it is adjusted to the data size. Default 0.0 represents choosing optimal value, depends on specific algorithm. Must be >= 0.'): 0.0, Param(parent='LogisticRegression_ce71e8a53e40', name='maxIter', doc='max number of iterations (>= 0).'): 10, Param(parent='LogisticRegression_ce71e8a53e40', name='predictionCol', doc='prediction column name.'): 'prediction', Param(parent='LogisticRegression_ce71e8a53e40', name='probabilityCol', doc='Column name for predicted class conditional probabilities. Note: Not all models output well-calibrated probability estimates! These probabilities should be treated as confidences, not precise probabilities.'): 'probability', Param(parent='LogisticRegression_ce71e8a53e40', name='rawPredictionCol', doc='raw prediction (a.k.a. confidence) column name.'): 'rawPrediction', Param(parent='LogisticRegression_ce71e8a53e40', name='regParam', doc='regularization parameter (>= 0).'): 0.01, Param(parent='LogisticRegression_ce71e8a53e40', name='standardization', doc='whether to standardize the training features before fitting the model.'): True, Param(parent='LogisticRegression_ce71e8a53e40', name='threshold', doc='Threshold in binary classification prediction, in range [0, 1]. If threshold and thresholds are both set, they must match.e.g. if threshold is p, then thresholds must be equal to [1-p, p].'): 0.5, Param(parent='LogisticRegression_ce71e8a53e40', name='tol', doc='the convergence tolerance for iterative algorithms (>= 0).'): 1e-06}
# We may alternatively specify parameters using a Python dictionary as a paramMap
paramMap = {lr.maxIter: 20}
paramMap[lr.maxIter] = 30 # Specify 1 Param, overwriting the original maxIter.
paramMap.update({lr.regParam: 0.1, lr.threshold: 0.55}) # Specify multiple Params.
# You can combine paramMaps, which are python dictionaries.
paramMap2 = {lr.probabilityCol: "myProbability"} # Change output column name
paramMapCombined = paramMap.copy()
paramMapCombined.update(paramMap2)
# Now learn a new model using the paramMapCombined parameters.
# paramMapCombined overrides all parameters set earlier via lr.set* methods.
model2 = lr.fit(training, paramMapCombined)
print("Model 2 was fit using parameters: ")
print(model2.extractParamMap())
Model 2 was fit using parameters:
{Param(parent='LogisticRegression_533be5a9d3e8', name='aggregationDepth', doc='suggested depth for treeAggregate (>= 2).'): 2, Param(parent='LogisticRegression_533be5a9d3e8', name='elasticNetParam', doc='the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty.'): 0.0, Param(parent='LogisticRegression_533be5a9d3e8', name='family', doc='The name of family which is a description of the label distribution to be used in the model. Supported options: auto, binomial, multinomial'): 'auto', Param(parent='LogisticRegression_533be5a9d3e8', name='featuresCol', doc='features column name.'): 'features', Param(parent='LogisticRegression_533be5a9d3e8', name='fitIntercept', doc='whether to fit an intercept term.'): True, Param(parent='LogisticRegression_533be5a9d3e8', name='labelCol', doc='label column name.'): 'label', Param(parent='LogisticRegression_533be5a9d3e8', name='maxBlockSizeInMB', doc='maximum memory in MB for stacking input data into blocks. Data is stacked within partitions. If more than remaining data size in a partition then it is adjusted to the data size. Default 0.0 represents choosing optimal value, depends on specific algorithm. Must be >= 0.'): 0.0, Param(parent='LogisticRegression_533be5a9d3e8', name='maxIter', doc='max number of iterations (>= 0).'): 30, Param(parent='LogisticRegression_533be5a9d3e8', name='predictionCol', doc='prediction column name.'): 'prediction', Param(parent='LogisticRegression_533be5a9d3e8', name='probabilityCol', doc='Column name for predicted class conditional probabilities. Note: Not all models output well-calibrated probability estimates! These probabilities should be treated as confidences, not precise probabilities.'): 'myProbability', Param(parent='LogisticRegression_533be5a9d3e8', name='rawPredictionCol', doc='raw prediction (a.k.a. confidence) column name.'): 'rawPrediction', Param(parent='LogisticRegression_533be5a9d3e8', name='regParam', doc='regularization parameter (>= 0).'): 0.1, Param(parent='LogisticRegression_533be5a9d3e8', name='standardization', doc='whether to standardize the training features before fitting the model.'): True, Param(parent='LogisticRegression_533be5a9d3e8', name='threshold', doc='Threshold in binary classification prediction, in range [0, 1]. If threshold and thresholds are both set, they must match.e.g. if threshold is p, then thresholds must be equal to [1-p, p].'): 0.55, Param(parent='LogisticRegression_533be5a9d3e8', name='tol', doc='the convergence tolerance for iterative algorithms (>= 0).'): 1e-06}
# Make predictions on test data using the Transformer.transform() method.
# LogisticRegression.transform will only use the 'features' column.
# Note that model2.transform() outputs a "myProbability" column instead of the usual
# 'probability' column since we renamed the lr.probabilityCol parameter previously.
prediction = model2.transform(test)
result = prediction.select("features", "label", "myProbability", "prediction") \
.collect()
for row in result:
print("features=%s, label=%s -> prob=%s, prediction=%s"
% (row.features, row.label, row.myProbability, row.prediction))
features=[-1.0,1.5,1.3], label=1.0 -> prob=[0.0570730417103402,0.9429269582896598], prediction=1.0 features=[3.0,2.0,-0.1], label=0.0 -> prob=[0.9238522311704104,0.07614776882958962], prediction=0.0 features=[0.0,2.2,-1.5], label=1.0 -> prob=[0.10972776114779444,0.8902722388522055], prediction=1.0
Pipline example: Decision tree classifier¶
from pyspark.ml import Pipeline
from pyspark.ml.classification import DecisionTreeClassifier
from pyspark.ml.feature import StringIndexer, VectorIndexer
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
# Load the data stored in LIBSVM format as a DataFrame.
data = spark.read.format("libsvm").load(f"file://{spark_home}/data/mllib/sample_libsvm_data.txt")
# Index labels, adding metadata to the label column.
# Fit on whole dataset to include all labels in index.
labelIndexer = StringIndexer(inputCol="label", outputCol="indexedLabel").fit(data)
# Automatically identify categorical features, and index them.
# We specify maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer = VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)
# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])
23/12/06 10:52:11 WARN [Thread-6] LibSVMFileFormat: 'numFeatures' option not specified, determining the number of features by going though the input. If you know the number in advance, please specify it via 'numFeatures' option to avoid the extra scan.
# Train a DecisionTree model.
dt = DecisionTreeClassifier(labelCol="indexedLabel", featuresCol="indexedFeatures")
# Chain indexers and tree in a Pipeline
pipeline = Pipeline(stages=[labelIndexer, featureIndexer, dt])
# Train model. This also runs the indexers.
model = pipeline.fit(trainingData)
# Make predictions.
predictions = model.transform(testData)
# Select example rows to display.
predictions.select("prediction", "indexedLabel", "features").show(5)
# Select (prediction, true label) and compute test error
evaluator = MulticlassClassificationEvaluator(
labelCol="indexedLabel", predictionCol="prediction", metricName="accuracy")
accuracy = evaluator.evaluate(predictions)
print("Test Error = %g " % (1.0 - accuracy))
treeModel = model.stages[2]
# summary only
print(treeModel)
+----------+------------+--------------------+ |prediction|indexedLabel| features| +----------+------------+--------------------+ | 1.0| 1.0|(692,[122,123,148...| | 1.0| 1.0|(692,[126,127,128...| | 1.0| 1.0|(692,[126,127,128...| | 1.0| 1.0|(692,[126,127,128...| | 1.0| 1.0|(692,[126,127,128...| +----------+------------+--------------------+ only showing top 5 rows Test Error = 0.0344828 DecisionTreeClassificationModel: uid=DecisionTreeClassifier_e98ee50f21dd, depth=1, numNodes=3, numClasses=2, numFeatures=692
Pipline example: Clustering¶
from pyspark.ml.clustering import KMeans
from pyspark.ml.evaluation import ClusteringEvaluator
# Loads data.
dataset = spark.read.format("libsvm").load(f"file://{spark_home}/data/mllib/sample_kmeans_data.txt")
23/12/06 10:52:39 WARN [Thread-6] LibSVMFileFormat: 'numFeatures' option not specified, determining the number of features by going though the input. If you know the number in advance, please specify it via 'numFeatures' option to avoid the extra scan.
# Trains a k-means model.
kmeans = KMeans().setK(2).setSeed(1)
model = kmeans.fit(dataset)
# Make predictions
predictions = model.transform(dataset)
# Evaluate clustering by computing Silhouette score
evaluator = ClusteringEvaluator()
silhouette = evaluator.evaluate(predictions)
print("Silhouette with squared euclidean distance = " + str(silhouette))
Silhouette with squared euclidean distance = 0.9997530305375207
# Shows the result.
centers = model.clusterCenters()
print("Cluster Centers: ")
for center in centers:
print(center)
Cluster Centers: [9.1 9.1 9.1] [0.1 0.1 0.1]
Model Selection with Cross-Validation¶
from pyspark.ml.classification import LogisticRegression
from pyspark.ml.evaluation import BinaryClassificationEvaluator
from pyspark.ml.feature import HashingTF, Tokenizer
from pyspark.ml.tuning import CrossValidator, ParamGridBuilder
# Prepare training documents, which are labeled.
training = spark.createDataFrame([
(0, "a b c d e spark", 1.0),
(1, "b d", 0.0),
(2, "spark f g h", 1.0),
(3, "hadoop mapreduce", 0.0),
(4, "b spark who", 1.0),
(5, "g d a y", 0.0),
(6, "spark fly", 1.0),
(7, "was mapreduce", 0.0),
(8, "e spark program", 1.0),
(9, "a e c l", 0.0),
(10, "spark compile", 1.0),
(11, "hadoop software", 0.0)
], ["id", "text", "label"])
# Configure an ML pipeline, which consists of tree stages: tokenizer, hashingTF, and lr.
tokenizer = Tokenizer(inputCol="text", outputCol="words")
hashingTF = HashingTF(inputCol=tokenizer.getOutputCol(), outputCol="features")
lr = LogisticRegression(maxIter=10)
pipeline = Pipeline(stages=[tokenizer, hashingTF, lr])
# We now treat the Pipeline as an Estimator, wrapping it in a CrossValidator instance.
# This will allow us to jointly choose parameters for all Pipeline stages.
# A CrossValidator requires an Estimator, a set of Estimator ParamMaps, and an Evaluator.
# We use a ParamGridBuilder to construct a grid of parameters to search over.
# With 3 values for hashingTF.numFeatures and 2 values for lr.regParam,
# this grid will have 3 x 2 = 6 parameter settings for CrossValidator to choose from.
paramGrid = ParamGridBuilder() \
.addGrid(hashingTF.numFeatures, [10, 100, 1000]) \
.addGrid(lr.regParam, [0.1, 0.01]) \
.build()
crossval = CrossValidator(estimator=pipeline,
estimatorParamMaps=paramGrid,
evaluator=BinaryClassificationEvaluator(),
numFolds=2) # use 3+ folds in practice
# Run cross-validation, and choose the best set of parameters.
cvModel = crossval.fit(training)
23/12/06 10:52:57 WARN [dag-scheduler-event-loop] InstanceBuilder$NativeBLAS: Failed to load implementation from:dev.ludovic.netlib.blas.JNIBLAS 23/12/06 10:52:57 WARN [dag-scheduler-event-loop] InstanceBuilder$NativeBLAS: Failed to load implementation from:dev.ludovic.netlib.blas.ForeignLinkerBLAS 23/12/06 10:52:57 WARN [Thread-189] BLAS: Failed to load implementation from: com.github.fommil.netlib.NativeSystemBLAS 23/12/06 10:52:57 WARN [Thread-189] BLAS: Failed to load implementation from: com.github.fommil.netlib.NativeRefBLAS
# Prepare test documents, which are unlabeled.
test = spark.createDataFrame([
(4, "spark i j k"),
(5, "l m n"),
(6, "mapreduce spark"),
(7, "apache hadoop")
], ["id", "text"])
# Make predictions on test documents. cvModel uses the best model found (lrModel).
prediction = cvModel.transform(test)
selected = prediction.select("id", "text", "probability", "prediction")
for row in selected.collect():
print(row)
Row(id=4, text='spark i j k', probability=DenseVector([0.2665, 0.7335]), prediction=1.0) Row(id=5, text='l m n', probability=DenseVector([0.9204, 0.0796]), prediction=0.0) Row(id=6, text='mapreduce spark', probability=DenseVector([0.4438, 0.5562]), prediction=1.0) Row(id=7, text='apache hadoop', probability=DenseVector([0.8587, 0.1413]), prediction=0.0)
%spark.stop_session
'success stop spark application application_1709108427864_0319'
Lab¶
- Run a logistic regression with airdelay data, or
- you can use your own data and run any machine learning models in Spark.