Bayesian Statistics and Computing

---

# Bayesian Statistics and Computing

## Lecture 9: Derivative Free Methods

#### *Yanfei Kang | BSC | Beihang University*

---

---
# Discontinuous Functions

- The Newton Method requires first and second derivatives.

- If derivatives are not available the they can be approximated by Quasi-Newton methods.

- What if the derivatives do not exist?

- This may occur if there are discontinuities in the function.

---
# Business Example

- Suppose the aim is to optimize income of the business by selecting the number of workers.

- In the beginning adding more workers leads to more income for the business.

- If too many workers are employed, they may be less efficient and the income of the company goes down.

---
# Business Example

<center>
![Continuous Function](./figures/contfunc.png)

---
# Business Example

- Now suppose that there is a tax that the company must pay.

- Companies with less than 50 workers do not pay the tax.

- Companies with more than 50 workers do pay the tax.

- How does this change the problem?

---
# Business Example

<center>
![Discontinuous Function](./figures/discontfunc.png)

---

---
# The Nelder Mead Algorithm

- Proposed by John Nelder and Roger Mead in 1965.

- The Nelder Mead algorithm is robust even when the functions are discontinuous.

- The idea is based on evaluating the function at the vertices of an `$n$`-dimensional simplex where `$n$` is the number of input variables into the function.

- For two dimensional problems the n-dimensional simplex is simply a triangle, and each corner is one vertex.

- In general there are `$n + 1$` vertices.

---
# A 2-dimensional simplex

<center>
![Nelder Mead](./figures/nm0.png)

---
# Step 1: Evaluate Function

- For each vertex `${\mathbf x_j}$` evaluate the function `$f({\mathbf x_j})$`.

- Order the vertices so that `$$f({\mathbf x_1})\leq f({\mathbf x_2})\leq\ldots\leq f({\mathbf x_{n+1}}).$$`

- Suppose that the aim is to  minimize the function, then `$f({\mathbf x_{n+1}})$` is the worst point.

- The aim is to replace `$f({\mathbf x_{n+1}})$` with a  better point.
   
   
---
# A 2-dimensional simplex

<center>                                           
![](./figures/nmf.png)

---
# Step 2: Find Centroid

- After eliminating the worst point `${\mathbf x_{n+1}}$`, compute the  centroid of the remaining `$n$` points `$${\mathbf x_0}=\frac{1}{n}\sum_{j=1}^{n}  {\mathbf x_j}.$$`

- For the 2-dimensional example the centroid will be in the middle of a line.

---
# Find Centroid

<center>      
![](./figures/nmcent.png)

---
# Step 3: Find reflected point

- Reflect the worst point around the centroid to get the  reflected point.

- The formula is: `$${\mathbf x_r}={\mathbf x_0}+\alpha({\mathbf x_0}-{\mathbf x_{n+1}}).$$`

- A common choice is `$\alpha=1$`.

- In this case the reflected point is the same distance from the centroid as the worst point.

---
# Find Reflected Point

<center>          
![](./figures/nmrefl.png)

---
# Find Reflected Point

<center>          
![](./figures/nmrefl1.png)

---
# Three cases

1. `$f({\mathbf x_1})\leq f({\mathbf x_r})<f({\mathbf x_n})$`
    - `${\mathbf x_r}$` is neither best nor worst point.
    
2. `$f({\mathbf x_r})<f({\mathbf x_1})$`
    - `${\mathbf x_r}$` is the best point.
    
3. `$f({\mathbf x_r})\geq f({\mathbf x_n})$`
    - `${\mathbf x_r}$` is the worst point.

---
# Case 1

A new simplex is formed with `${\mathbf x_{n+1}}$` replaced by the reflected point `${\mathbf x_{r}}$`.  Then go back to step 1.

---
# Case 1

![](./figures/nmrefl2.png)

---
# Case 1

<center>         
![](./figures/nmrefl3.png)

---
# Case 2

In Case 2, `$f({\mathbf x_r})<f({\mathbf x_1})$`. A good direction has been found so we expand along that direction $$ {\mathbf x_e}={\mathbf x_0}+\gamma({\mathbf x_r}-{\mathbf x_0}).$$
                                                                     
A common choice is `$\gamma=2$`.

---
# Case 2

<center>          
![](./figures/nmexpansion1.png)

---
# Case 2

<center>         
![](./figures/nmexpansion2.png)

---
# Choosing the Expansion Point

- Evaluate `$f({\mathbf x_e})$`.

- If `$f({\mathbf x_e}) < f({\mathbf x_r})$`:
    - The expansion point is better than the reflection point. Form a new simplex with the expansion point.
    
- If `$f({\mathbf x_r})\leq f({\mathbf x_e})$`:
    - The expansion point is not better than the reflection point. Form a new simplex with the reflection point.
    
---
# Keep Expansion Point

<center>          
![](./figures/nmexpansion3.png)

## Keep Relection Point

<center>          
![](./figures/nmexpansion4.png)

---
# Case 3

<center>          
![](./figures/nmcontraction1.png)

---
# Case 3

Case 3 implies that there may be a valley between `${\mathbf x_{n+1}}$` and `${\mathbf x_{r}}$`.

---
# Case 3

So find the contracted point.  A new simplex is formed with the contraction point if it is better than `${\mathbf x_{n+1}}$`:
        `$${\mathbf x_c}={\mathbf x_0}+\rho({\mathbf x_{n+1}}-{\mathbf x_0}).$$`

A common choice is `$\rho=0.5$`.
---
# Case 3

<center>          
![](./figures/nmcontraction2.png)

---
# New Simplex

<center>         
![](./figures/nmcontraction3.png)

---
# Shrink

If `$f({\mathbf x_{n+1}})\leq f({\mathbf x_{c}})$` then contracting away from the worst point does not lead to a better point.  In this case the function is too irregular a smaller simplex might be used.

---
# Contraction Point is worst

<center>         
![](./figures/nmshrink1.png)

---
# New Simplex

<center>         
![](./figures/nmshrink2.png)

---
# Shrink

Shrink the simplex `$${\mathbf x_i}={\mathbf x_1}+\sigma({\mathbf x_i}-{\mathbf x_1}).$$`

A popular choice is `$\sigma=0.5$`.

---
# Summary

- Order points.

- Find centroid.

- Find reflected point.

- Three cases:
    1. Case 1: `$f({\mathbf x_1}) \leq f({\mathbf x_r})<f({\mathbf x_n})$`, keep `${\mathbf x_r}$`.
    2. Case 2: `$f({\mathbf x_r}) < f({\mathbf x_1})$`, find `$\mathbf x_e$`.
        - If `$f({\mathbf x_e})<f({\mathbf x_r})$` then keep `$\mathbf x_e$`.
        - Otherwise keep `$\mathbf x_r$`.
    3. Case 3: `$f({\mathbf x_r}) \geq f({\mathbf x_n})$`, find `$\mathbf x_c$`.
        - If `$f({\mathbf x_c})<f({\mathbf x_{n+1}})$` then keep `$\mathbf x_c$`.
        - Otherwise shrink.

---
# Exercise

- Write in R one single iteration of Nelder Mead.

- Don't worry about using a loop just yet.  Try to get code that just does the first iteration.

- Don't worry about the stopping rule yet either.

- Try different starting simplex.

---
# Use pseudo-code

<center>         
![](./figures/nmcode.png)

---
# Animation

<center>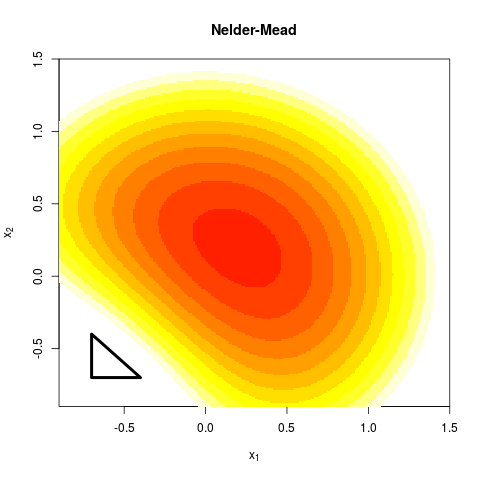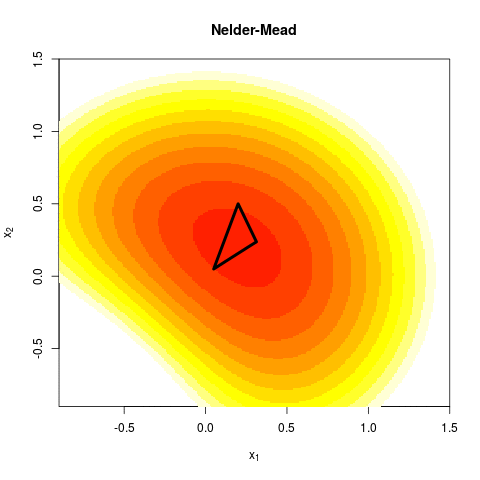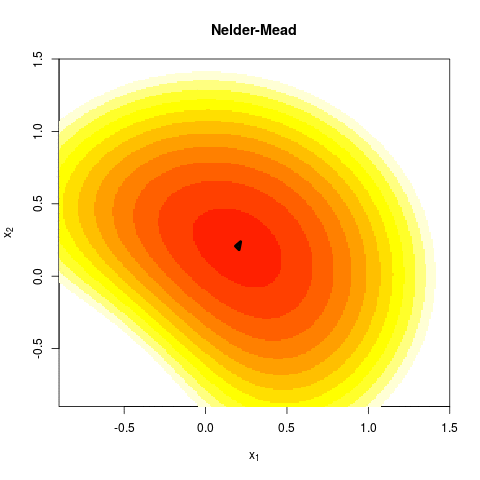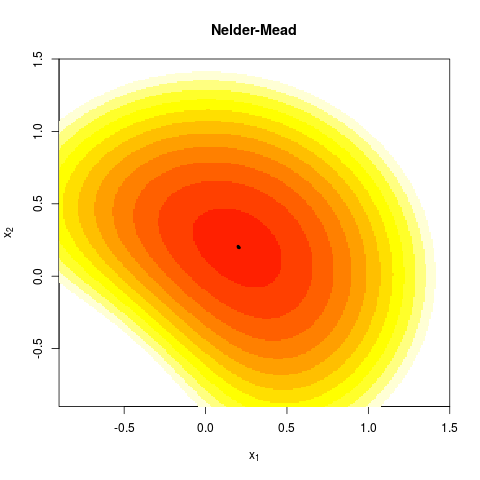
![](./figures/movie2.gif)

---
# Stopping Rule for Nelder Mead

- As Nelder Mead gets close to (or reaches) the minimum, the simplex gets smaller and smaller.

- One way to know that Nelder Mead has converged is by looking at the volume of the simplex.

- To work out the volume requires some understanding between the relationship between matrix algebra and geometry.

---
# Stopping Rule for Nelder Mead                                     
- Choose the vertex `${\mathbf x_{n+1}}$` (although choosing any other vertex will also work).

- Build the matrix                                                                                  `$\tilde{X}=\left({\mathbf x_1}-{\mathbf x_{n+1}},{\mathbf x_2-{\mathbf x_{n+1}}},\ldots, {\mathbf x_{n}-{\mathbf x_{n+1}}}\right)$`.
                          
- The volume of the simplex is `$\frac{1}{2}|det(\tilde{X})|$`.

---
# Why?

<center>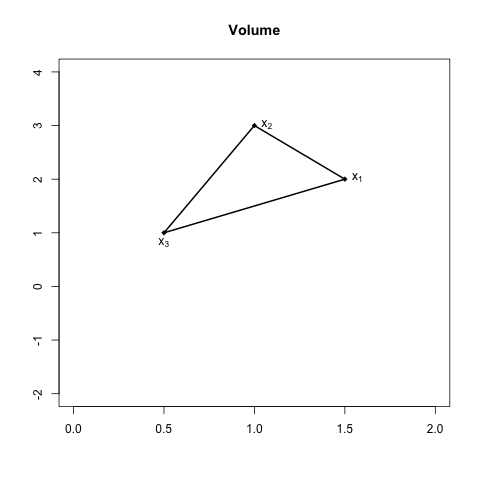          
![](./figures/geom1.png)

---
# Traslate

<center>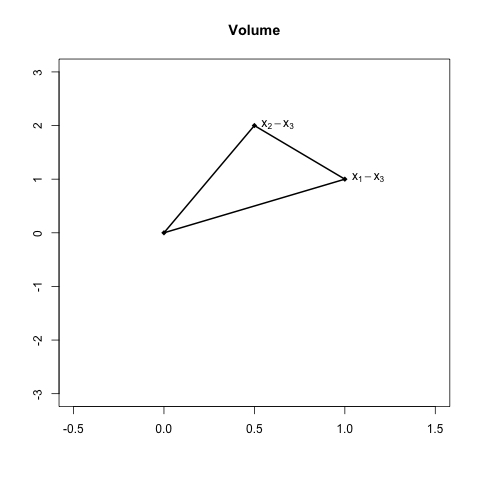         
![](./figures/geom2.png)

---
# Determinant=Area of Trapezoid

<center>         
![](./figures/geom3.png)

## Triangle=Half Trapezoid

<center>          
![](./figures/geom4.png)

---
# Alternative formula

Some of you may have learnt the formula for the area of a triangle as:

`$$\frac{1}{2}\left|det\left(\begin{array}{ccc}
{\mathbf x_1}& {\mathbf x_2}& {\mathbf x_3}\\
1 & 1 & 1\end{array}\right)\right|.$$`

The two approaches are equivalent.

---
## Notes

1. Nelder-Mead is generally used for parameter selection in Machine Learning. It will work reasonably well for non-differentiable functions.

2. It tends to get stuck in local optima.

3. Python [Scipy](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-neldermead.html) implementation of Nelder-Mead.

4. There is a best way to choose the initial simplex in the Nelder-Mead method. Please refer to the supplementary material and the R package [neldermead](https://cran.r-project.org/web/packages/neldermead/neldermead.pdf) for further information.

---
# Nelder Mead in `optim()`

- Nelder Mead is the default algorithm in the R function `optim()`.

- It is generally slower than Newton and Quasi-Newton methods but is more stable for functions that are not smooth.

- Including the argument `control=list(trace, REPORT=1)` will print out details about each step of the algorithm.

- Slight different terminology is used for example 'expansion' is called 'extension'

---
# Summary

- You should now be familiar with
    - Newton's Method
    - Quasi Newton Method
    - Nelder Mead

- Hopefully you also improved your coding skills!

---
# Summary

- If you can evaluate derivatives and Hessians then do so when implementing Newton and Quasi-Newton methods.

- If there are discontinuities in the function then Nelder Mead may work better.

- In any case the best strategy is to optimize using more than one method to check that results are robust.

- Also pay special attention to starting values. A good strategy is to check that results are robust to a few different choices of starting values.

---
class: inverse, center, middle
# Lab 7: Coding Nelder Mead

---
# Lab 7

1. Find the minimum of the function `$f({\mathbf x})=x_1^2+x_2^2$`. Try different initial values.

2. Re-do the linear regression example with Nelder Mead.