Bayesian Statistics and Computing

class: left, bottom, inverse, title-slide

# Bayesian Statistics and Computing
## Lecture 12: Introduction to Bayesian Computing
### Yanfei Kang
### 2020/03/15 (updated: 2020-04-01)

---

# Strategies to summarize posterior

1. If we have familiar distributions, we can simply **simulate** samples in R.

2. **Grid approximation**.
    - Compute values of the posterior on a grid of points.
    - Approximate the continuous posterior by a discrete posterior.
    - Applicable for one- and two-parameter problems.
    
---
# Bayesian computing

- Bear in mind that given the prior and data, the posterior is fixed and a Bayesian analysis really boils down to **summarizing the posterior**.

- Summarizing a `$p$`-dimensional posterior distribution is
challenging for large `$p$`.

- In 80's, Bayesian computing was unable to do this for
more than a few parameters.

- In the 90’s, new algorithms were developed that
revolutionized Bayesian statistics.

---
# Approaches to Bayesian Computing

1. Just use a point estimate: Maximum a Posteriori (MAP) estimate.

2. Approximate the posterior as Gaussian.

3. Numerical integration.

4. Markov Chain Monte Carlo (MCMC) sampling.

**We will focus on 1-3 for this lecture.**

---
class: inverse, center, middle
# MAP

---
# MAP

- Approximate based on posterior modes.

- Maximize the posterior
`$$\hat{\boldsymbol{\theta}}=\underset{\boldsymbol{\theta}}{\operatorname{argmax}} p(\boldsymbol{\theta} | \mathbf{Y})=\underset{\boldsymbol{\theta}}{\operatorname{argmax}} \log [f(\mathbf{Y} | \boldsymbol{\theta})]+\log [p(\boldsymbol{\theta})].$$`

- This is similar to the maximum likelihood estimation but
includes the prior.

- And you already know optimization.

---
# Lab 9.1

Say `$Y|\theta \sim \text{Poisson}(N\theta),$` and `$\theta \sim \text{Gamma}(a, b)$`, find `$\hat{\theta}_{MAP}$`.

---
class: inverse, center, middle
# Approximate the posterior as Gaussian

---
# Bayesian Central Limit Theorem

- We can actually approximate the posterior as Gaussian.

- Replies on **Berstein-Von Mises Theorem**: when the sample size is very large, the posterior does not depend on the prior.

- **Bayesian Central Limit Theorem (Bayesian CLT)**: when the sample size is very large, `$\theta|Y \sim \text{Normal}$`.

---
# Bayesian CLT

- For large `$n$`, `$$\boldsymbol{\theta} \sim \operatorname{Normal}\left[\hat{\boldsymbol{\theta}}_{M A P}, \mathbf{I}\left(\hat{\boldsymbol{\theta}}_{M A P}\right)^{-1}\right].$$`

- The `$(j, k)$`-th element of `$\mathbf{I}$` is `$-\frac{\partial^{2}}{\partial \theta_{j} \partial \theta_{k}} \log [p(\boldsymbol{\theta} | \mathbf{Y})],$` evaluated at `$\hat{\theta}_{MAP}$`.

- Then we can do everything we do for normal distribution, e.g., sd, intervals etc.

---
# Lab 9.2

Say `$Y | \theta \sim \text { Binomial }(n, \theta)$`, and `$\theta \sim \operatorname{Beta}(0.5,0.5)$`, find the
Gaussian approximation for `$p(\theta|Y)$`.

---
# Lab continued

- The exact posterior is `$\theta | Y \sim \operatorname{Beta}(Y+1 / 2, n - Y +1 / 2)$`.

- MAP estimator `$\hat{\theta}=A /(A+B),$` where `$A = Y - 1/2$` and `$B = n - Y - 1/2$`.

- The posterior variance is approximated as `$\frac{1}{\frac{A}{\hat{\theta}^2}+\frac{B}{(1-\hat{\theta})^2}}$`.

---
# Approximation in a small sample case

.pull-left[

```r
theta <- seq(0.001, 0.999, 0.001)  # Grid of thetas for plotting
Y <- 2
n <- 5
# Compute the posterior mean and Fisher information matrix
A <- Y - 0.5
B <- n - Y - 0.5
theta_MAP <- A/(A + B)
Info <- A/theta_MAP^2 + B/(1 - theta_MAP)^2
# Plot the true and approximate posteriors
post1 <- dbinom(Y, n, theta) * dbeta(theta, 0.5, 0.5)
post1 <- post1/sum(post1)
post2 <- dnorm(theta, theta_MAP, sqrt(1/Info))
post2 <- post2/sum(post2)
plot(theta, post1, type = "l", lwd = 2, xlab = expression(theta), ylab = "Posterior")
abline(v = theta_MAP, col = 3, lwd = 2)
lines(theta, post2, col = 2, lwd = 2)
legend("topright", c("Exact", "CLT", "MAP"), bty = "n", col = 1:3, cex = 1.5, lwd = 2)
```
]

.pull-right[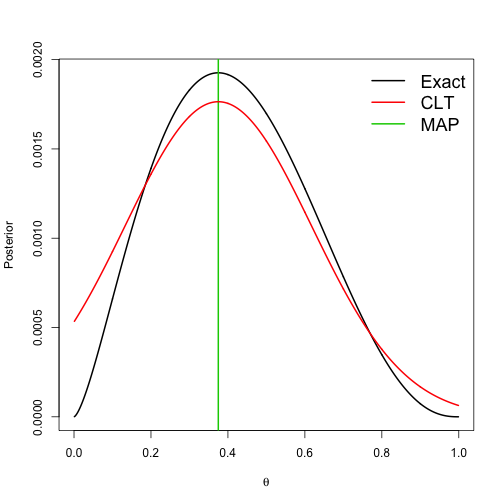
![](BSC-L12-computing_files/figure-html/unnamed-chunk-1-1.png)
]

---
# Approximation in a medium sample case

.pull-left[

```r
theta <- seq(0.001, 0.999, 0.001)  # Grid of thetas for plotting
Y <- 3
n <- 10
# Compute the posterior mean and Fisher information matrix
A <- Y - 0.5
B <- n - Y - 0.5
theta_MAP <- A/(A + B)
Info <- A/theta_MAP^2 + B/(1 - theta_MAP)^2
# Plot the true and approximate posteriors
post1 <- dbinom(Y, n, theta) * dbeta(theta, 0.5, 0.5)
post1 <- post1/sum(post1)
post2 <- dnorm(theta, theta_MAP, sqrt(1/Info))
post2 <- post2/sum(post2)
plot(theta, post1, type = "l", lwd = 2, xlab = expression(theta), ylab = "Posterior")
abline(v = theta_MAP, col = 3, lwd = 2)
lines(theta, post2, col = 2, lwd = 2)
legend("topright", c("Exact", "CLT", "MAP"), bty = "n", col = 1:3, cex = 1.5, lwd = 2)
```
]

.pull-right[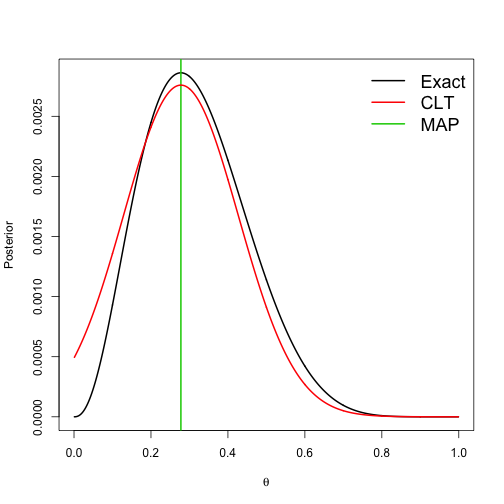
![](BSC-L12-computing_files/figure-html/unnamed-chunk-2-1.png)
]

---
# Approximation in a large sample case

.pull-left[

```r
theta <- seq(0.001, 0.999, 0.001)  # Grid of thetas for plotting
Y <- 30
n <- 100
# Compute the posterior mean and Fisher information matrix
A <- Y - 0.5
B <- n - Y - 0.5
theta_MAP <- A/(A + B)
Info <- A/theta_MAP^2 + B/(1 - theta_MAP)^2
# Plot the true and approximate posteriors
post1 <- dbinom(Y, n, theta) * dbeta(theta, 0.5, 0.5)
post1 <- post1/sum(post1)
post2 <- dnorm(theta, theta_MAP, sqrt(1/Info))
post2 <- post2/sum(post2)
plot(theta, post1, type = "l", lwd = 2, xlab = expression(theta), ylab = "Posterior")
abline(v = theta_MAP, col = 3, lwd = 2)
lines(theta, post2, col = 2, lwd = 2)
legend("topright", c("Exact", "CLT", "MAP"), bty = "n", col = 1:3, cex = 1.5, lwd = 2)
```
]

.pull-right[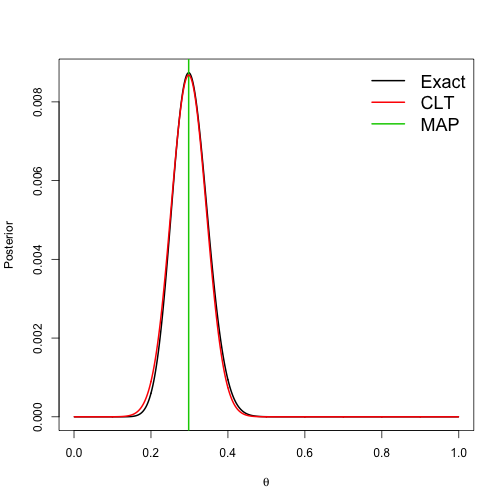
![](BSC-L12-computing_files/figure-html/unnamed-chunk-3-1.png)
]

---
class: inverse, center, middle
# Numerical integration

---
# Numerical integration

- Many posterior summaries of interest are integrals over the
posterior.

- We usually can't solve integrals analytically.

- A grid approximation is a crude approach.

- Gaussian quadrature is better.

- The Iteratively Nested Laplace Approximation (INLA) is an
even more sophisticated method.

- Does not work well for large `$p$`.

---
class: inverse, center, middle
# Summary

---
# Summary

- Bayesian inference requires summarizing the posterior distribution.

- When there are more than a few parameters, this requires advanced computational tools.

- Some methods that are deterministic.
    - MAP
    - Bayesian CLT
    - Numerical Integration
    
- Monte Carlo methods are more general (next lecture).