第 10 章 统计计算中的线性代数方法
10.1 介绍
矩阵在求解线性方程式方面有着悠久的应用历史,但直到1800年代才被称为数组。中文于公元前10至2世纪写成的《九章算术》是使用数组方法求解联立方程的第一个例子,《九章算术》甚至包括行列式概念。 1545年,意大利数学家杰拉莫莫·卡尔达诺(Gerolamo Cardano)出版了Ars Magna,将这种方法带到了欧洲。日本数学家关树(Seki)在1683年使用相同的数组方法求解联立方程。荷兰数学家扬·德·维特(Jan de Witt)在1659年出版的《曲线的元素》(Elements of Curves,1659年)一书中使用数组表示变换。在1700年至1710年之间,Gottfried Wilhelm Leibniz公开了使用数组来记录信息或解决方案,并尝试了50多种不同的数组系统。
据记载,詹姆士·约瑟夫·西尔维斯特(James Joseph Sylvester)在1850年提出了“矩阵”一词(拉丁语为“子宫”,源自母体),他将矩阵理解为对象。有趣的是,现代编程软件普遍把矩阵认为是对象。
矩阵无处不在,比如任何可以放在 Excel 电子表格中的东西都是矩阵,文本和图像也可以用矩阵表示,线性回归的估计可以通过矩阵运算得到,谷歌的页面排序是通过特征分解来计算的。随着 5G 时代的到来及数据的爆发式增长,传统的线性代数方法很难完成大规模计算,因此,了解矩阵计算的数值算法及其应用,可以帮助提供更高效的解决方案。例如,近似矩阵计算通常比精确矩阵计算快几千倍。20世纪的十大科学与工程算法就包括矩阵分解方法和 QR算法(我们将要在后续章节中介绍)。
矩阵计算通常可以使用不同的技术方法,比如直接算法或迭代方法。例如,可以通过找到当\(n\)趋于无穷大时收敛到特征向量的向量\(x_n\)的序列来获得方阵的特征向量。为了针对每个特定问题选择最合适的算法,重要的是确定所有可用算法的有效性和精度。研究这些问题的领域称为数值线性代数。在许多实际情况下,一个重要的矩阵是稀疏矩阵,即大多数条目为零的矩阵。例如,针对共轭梯度法,有专门针对稀疏矩阵\(A\)求解线性系统\(Ax = b\)的算法。
几乎所有当前使用的编程语言都提供矩阵运算。矩阵操纵是计算机最早的数值应用之一。最初的Dartmouth BASIC语言自1964年第二版实施以来就在阵列中内置了用于矩阵算术的命令。早在1970年代,某些工程台式计算机(例如HP 9830)就装有ROM盒,以添加用于矩阵的BASIC命令。某些计算机语言(例如APL)被设计为处理矩阵,并且各种数学程序可用于辅助矩阵计算。
10.2 特征分解
10.2.1 特征分析
一般来讲,一个 \(n \times n\) 的矩阵 \(A\) 乘以一个向量 \(x\) 之后得到的向量 \(Ax\) 既改变 \(x\) 的长度,也改变其方向。但是,存在某些向量 \(x\),使得 \(Ax\) 只改变 \(x\) 的长度而不改变其方向:即满足 \(Ax = \lambda x\),那么 \(\lambda\) 是 \(A\) 的特征值,\(x\) 是其特征向量。在二维情况下的特征分析(eigenanalysis)过程如图10.1所示2。
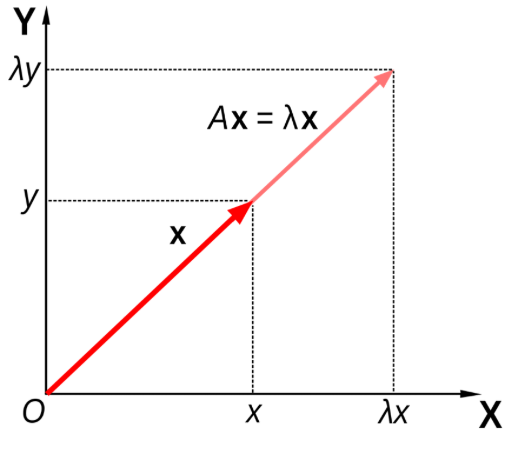
图10.1: 二维矩阵的特征分析
10.2.2 矩阵的特征分解过程
特征分解(eigendecomposition)又叫谱分解(Spectral decomposition),是把一个矩阵根据其特征值和特征向量分解的过程。只有可以正交化的矩阵才可以进行特征分解。
如果 \(n \times n\) 的矩阵 \(A\) 具有 \(n\) 个线性独立的特征向量,那么 \(A\) 是可以正交化的,此时 \(A\) 的特征分解为:
\[A = Q \Lambda Q^{-1},\]其中 \(Q\) 是一个 \(n \times n\) 的方阵,其第 \(i\) 列对应 \(A\) 的第 \(i\) 个特征向量 \(q_{i}\),\(\Lambda\) 是一个对角阵,其对角线上的元素对应 \(A\) 的 \(n\) 个特征值:\(\Lambda_{ii} = \lambda_{i}\)。
注意:只有可以正交化的矩阵才可以进行上述特征分解。
如果 \(A\) 是一个 \(n \times n\) 的实对称阵,那么
- \(A\) 的 \(n\) 个特征根都为实数。
- \(A\) 有 \(n\) 个互相正交的特征向量。
因此,一个实对称矩阵 \(A\) 是可以正交化的,也就可以进行特征分解。
如果矩阵 \(A\) 不可以对角化,那么可以通过 Schur 分解将其进行三角化:
\[A = QUQ^{-1},\]其中 \(Q\) 是一个正交阵,\(U\) 是一个上三角矩阵,其对角线上的元素对应 \(A\) 的特征值。
10.3 奇异值分解
对于一个方阵 \(A\) 而言,是可以对角化或者三角化的。这在矩阵计算中非常有用。但是对于一个非方阵而言,我们并不能对其进行特征分解,这个时候我们怎么办呢?在本节中,我们将学习对任何矩阵适用的矩阵分解方法 — 奇异值分解 (Singular Value Decomposition,简称 SVD)。
10.3.1 奇异值(Singular values)和奇异向量(Singular vectors)
奇异值 \(\sigma\) 是矩阵\(A^TA\)(对称方阵)特征根的平方根。对应的一对奇异向量(\(u\) 和 \(v\))满足
\[A v = \sigma u.\]
我们可以将矩阵的特征分解拓展,矩阵 \(A\) 的特征分解 \(A=Q\Lambda Q^T\) 对每个特征值只涉及到一个特征向量,我们如果将其拓展到奇异值和奇异向量,就有了一个一般矩阵的奇异值分解方法。
10.3.2 奇异值分解
对于 \(A \in \mathcal{R}^{m \times n}\),假设 \(m \geq n\),那么存在正交阵
\[U = [u_1, \cdots, u_m] \in \mathcal{R}^{m\times m}\] 和
\[V = [v_1, \cdots, v_n] \in \mathcal{R}^{n\times n},\]
使得
\[\begin{equation} U^TAV = \Sigma = \text{diag}\{\sigma_1, \cdots, \sigma_p\} \in \mathcal{R}^{m\times n}, \tag{10.1} \end{equation}\]
其中 \(p = \min\{m, n\}\), \(\sigma_1 \geq \dots \geq \sigma_p \geq 0\)。\(\Sigma\) 是一个对角阵,对角线上的非负元素降序排列,其最后 \(m - n\) 行的元素为零。 \(\sigma_j\) 为奇异值,\(u_j\) 和 \(v_j\) 分别为左右奇异向量。
公式 (10.1)经过变换,我们可以得到
\[\begin{equation} A = U\Sigma V^T. \tag{10.2} \end{equation}\]
因为 \(\Sigma\) 的最后 \(m - n\) 行的元素为零,因此 SVD 分解也可以写为
\[\begin{equation} A = U\Sigma V^T = \left(\begin{array}{cc}U_1 & U_2\end{array}\right) \left(\begin{array}{cc} D & \\ & 0 \end{array}\right) \left(\begin{array}{cc}V_1^T & V_2^T\end{array}\right) = U_1^TDV_1^T, \tag{10.3} \end{equation}\]其中 \(D = \text{diag}\{\alpha_1, \cdots, \alpha_r\} \in \mathcal{R}^{r\times r}\),\(\sigma_r > 0\),\(r = \text{rank}(A)\)。
10.4 奇异值分解的应用
10.4.1 矩阵的低秩估计
根据公式 (10.3),\(A\) 也可以写成外积加和形式
\[A = \Sigma_{i = 1}^r \sigma_i u_u v_i^T = \alpha_1 u_1 v_1^T + \cdots + \alpha_r u_r v_r^T.\]如果我们只取前 \(k,~ 1 \leq k \leq r\) 个加和,我们可以得到
\[A_k = \Sigma_{i = 1}^{k < r} \sigma_i u_u v_i^T = \alpha_1 u_1 v_1^T + \cdots + \alpha_k u_k v_k^T,\]其中 \(A_k\) 的秩为 \(k\)。如果奇异值 \(\sigma_{k+1}, \cdots, \sigma_r\) 很小的话,\(A\) 和 \(A_k\) 之间的差别即 \(A - A_k\) 也很小。并且 \(||A - A_k|| = \sigma_{k+1}\),这通常被用作矩阵低秩估计的误差(Matrix Approximation Error)。这说明如果 \(\sigma_{k+1}\) 很小的话,用 \(A_k\) 来估计 \(A\) 就相当精确。
10.4.2 图像压缩
在许多应用(如网页设计)中,我们经常需要传输和存储图像。图像越小,传输和存储的成本就越低。因此,我们经常需要应用数据压缩技术来减少图像所消耗的存储空间。一种方法是对图像矩阵进行奇异值分解(SVD)。通过对图像矩阵的低秩估计,来完成图像压缩。对于一个 \(m\times n\) 的矩阵 \(A\),其存储大小为 \(m\times n\) 个像素点,经过压缩后的 \(A_k\),存储像素点变为 \(m\times k + k + k\times n = k \times (1 + m + n)\)。
例3.1 基于矩阵的低秩估计对以下本书作者进行压缩。

library(jpeg)
ykang <- readJPEG('./figs/ykang.jpg')
r <- ykang[,,1]
g <- ykang[,,2]
b <- ykang[,,3]
ykang.r.svd <- svd(r)
ykang.g.svd <- svd(g)
ykang.b.svd <- svd(b)
rgb.svds <- list(ykang.r.svd, ykang.g.svd, ykang.b.svd)
for (j in seq.int(4, 200, length.out = 8)) {
a <- sapply(rgb.svds, function(i) {
ykang.compress <-
i$u[,1:j] %*%
diag(i$d[1:j]) %*%
t(i$v[,1:j])
}, simplify = 'array')
writeJPEG(a, paste('./figs/', 'ykang_svd_rank_',
round(j,0), '.jpg', sep=''))
}以下四张压缩后的图像的秩分别为 200、116 和 32。他们分别需要存储多少个像素点?和原图像相比,他们分别的压缩比例又是多少?



10.5 数值方法
我们在《线性代数》课程中学过通过求矩阵特征多项式的根来求矩阵特征值,从而得到对应的特征向量。然而,在工业规模的大型矩阵中,这种方法是不可行的,必须通过其他方法得到特征值。幸运的是,我们可以通过求矩阵特征值和特征向量的数值技术来解决这一问题,其中一些技术属于迭代方法的范畴。这些方法的工作原理是反复地对特征向量或特征值进行精细化,只要逼近达到适当的精度,就可以终止。迭代法也是现代特征值计算的基础。
10.5.1 幂方法(Power method)
幂方法是计算矩阵极值特征值和相关特征向量的经典方法之一。在实践中,计算
对于一个 \(n \times n\) 的矩阵 \(A\),如果 \(q\) 是其对应于特征值 \(\lambda\) 的特征向量,那么 \(Aq = \lambda q\)。更一般的,\(A^kq = \lambda^kq\),这也是幂方法的理论基础。假设 \(A\) 的 \(n\) 个实数特征值为 \(|\lambda_1| > |\lambda_2| > \cdots > |\lambda_n|\),其对应的互相独立的特征向量分别为 \(q_1, \cdots, q_n\)。\(\lambda_1\) 和 \(\lambda_n\) 为 \(A\) 的两个极值特征值,那么幂方法的过程如下。
选择一个初始 \(x_0\),左乘矩阵 \(A\) 得到 \(x_1 = Ax_0\),再次左乘 \(A\),得到 \(x_2 = Ax_1\),以此类推:
\[x_1 = Ax_0;~x_2 = Ax_1 = A^2x_0; \cdots; x_k = A^kx_0.\]
那么幂方法为什么最终会收敛呢?我们来看一下其背后的原理。
因为 \(q_1, \cdots, q_n\) 互相独立,所以对于向量 \(x_0\) 可以写为:
\[x_0 = c_1 q_1 + \cdots + c_nq_n,\]
那么,
\[\begin{align*} A^kx_0 & = c_1 \lambda_1^k q_1 + \cdots + c_n\lambda_n^kq_n,\\ & = \lambda_1^k (c_1q_1 + \cdots + c_n(\frac{\lambda_n}{\lambda_1})^kq_n). \end{align*}\]因为我们假设 \(\lambda_1\) 为绝对值最大的特征值,因此对于 \(i = 2, \cdots, n\),
\[\lim\limits{k \rightarrow \infty}(\frac{\lambda_n}{\lambda_1})^k = 0,\]所以当 \(k \rightarrow \infty\) 时,\(A^kx_0 \rightarrow c_1\lambda_1^kq_1\),其和 \(q_1\) 的方向一致。
因为随着幂方法的不断迭代,\(x_0^k\) 的元素会越来越大,但是其实我们只关心的是特征向量的方向,所以在实践中通常使用标准化的幂方法。
标准化的幂方法
选择一个初始 \(q_0 = \frac{x_0}{||x_0||}\)>
对于 \(k = 1, 2, \cdots\) 重复以下过程,
- 计算 \(x_k = Ax_{k-1}\),
- 标准化 \(q_k = x_k/||x_k||\),
- 计算 \(\lambda_k = q_k^TAq_k\)。
10.6 案例:谷歌页面排序(PageRank)算法
什么是 PageRank 算法?
PageRank 算法是特征分解方法在现实中的典型应用,很好地解决了网页搜索结果的排序问题。PageRank 算法由 Google 的创始人拉里·佩奇(Larry Page)和谢尔盖·布林(Sergey Brin)在1998年提出。有趣的是,PageRank 中的 Page 意为页面,更是提出者之一拉里·佩奇(Page)的姓。
当我们进行搜索时,搜索引擎会找到与搜索关键词相关的页面(Page),如何对这些页面(Page)进行排序(Rank),让使用者更容易看到重要的页面?这就是 PageRank 算法所要解决的问题。
PageRank 算法如何进行排序?
PageRank简单来讲,就是让所有页面进行投票表决,依据得票高低对页面进行排名。在互联网世界中,选票就是网页上的超链接(hyperlink),每个页面会给它链接的\(m\)个页面各投\(\frac{1}{m}\)票,每票的权重由投票页面本身的重要性决定。
举例来说,假如我们找到五个网页,他们之间的链接关系如下图所示:
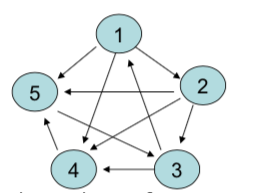
图10.2: 仅有五个页面的链接关系示例。
假设五个页面的重要性得分分别为 \(r_1,r_2,r_3,r_4,r_5\),那么按照上面的思路,我们可以得到以下五个等式:
\[\begin{align*} r_1 &= \frac{1}{2} r_3, \\ r_2 &= \frac{1}{3} r_1, \\ r_3 &= \frac{1}{3} r_2 + r_5, \\ r_4 &= \frac{1}{3} r_1 + \frac{1}{3} r_2 + \frac{1}{2}r_3, \\ r_5 &= \frac{1}{3} r_1 + \frac{1}{3} r_2 + r_4. \end{align*}\]
如果能计算出\(\mathbf{r}=\{r_1,r_2,r_3,r_4,r_5\}\),即可对页面按照\(r_i\)由高到低进行排序。
这里就需要使用到特征分解。
首先用邻接矩阵 \(\mathbf{A}\) 表示各页面之间的链接关系,
\[ \mathbf{A}=\left(\begin{array}{lllll} 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \end{array}\right) \]矩阵第 \(i\) 行第 \(j\) 列的元素为 1 表示页面 \(i\) 可以链接到页面 \(j\),为 0 表示不能链接。将矩阵 \(\mathbf{A}\) 按行归一化(normalize),得到以下形式的矩阵 \(\mathbf{B}\):
\[ \mathbf{B}=\left(\begin{array}{lllll} 0 & 1/3 & 0 & 1/3 & 1/3 \\ 0 & 0 & 1/3 & 1/3 & 1/3 \\ 1/2 & 0 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \end{array}\right) \]这样,上面复杂的方程组可以使用矩阵形式表示:
\[ \mathbf{r}=\mathbf{r}\mathbf{B} \]上式左右两边分别转置:
\[ \mathbf{r^T}=\mathbf{B^T}\mathbf{r^T} \]可以发现,\(\mathbf{r}\) 实际上是矩阵 \(\mathbf{B^T}\) 特征值为1时对应的特征向量。
因此,只需要构建邻接矩阵,经过简单的变化后进行特征分解,即可对重要性进行衡量,进而对页面进行排序。
简单将以上过程实现:
A <- matrix(c(0,0,1,0,0, 1,0,0,0,0, 0,1,0,0,1,
1,1,1,0,0, 1,1,0,1,0),5,5)
B <- A/apply(A,1,sum)对矩阵 \(\mathbf{B^{T}}\) 进行特征分解:
eigen.results <- eigen(t(B))列归一化后,矩阵 \(\mathbf{B^T}\) 的最大特征值为1,得到对应的特征向量即为 \(\mathbf{r}\):
eigen.results$values[1]
#> [1] 1+0i
r <- eigen.results$vectors[,1]
abs(r)
#> [1] 0.3048 0.1016 0.6096 0.4402 0.5757对重要性得分进行排序(由高到低):
order(abs(r),decreasing = T)
#> [1] 3 5 4 1 2现实中 PageRank 怎么实现?
在上面的例子中,面对矩阵的特征分解,我们直接使用了R语言中的命令:
但在实际中,面对数以亿计的网页,我们需要更高效的算法和计算“工具”。这里的高效算法就是 Power Method,高效的计算“工具”就是 MapReduce。
假设我们得到一个处理后的\(N \times N\)的邻接矩阵\(\mathbf{B}\):
- 设置 \(r_0\) 的初始值为\((\frac{1}{N},\frac{1}{N}...,\frac{1}{N})\)。
- 对于第 \(k\) 步循环:
- 计算\(x_k=r_{k-1} B\),
- 将\(x_k\)归一化,得到\(r_k=x_k/||x_k||\)。
- 重复上面的循环直到 \(r_k\) 收敛,将 \(r_k\) 作为最终重要性得分结果。
以上就是 Power Method 步骤(这个问题中,它有一个更直观的解释,我们会在下一小节介绍)。但不要认为这是一个简单的过程,在实际应用中,由于找到的网页数以亿计,这个邻接矩阵会变得相当之大,循环迭代第一步 \(x_k=r_{k-1}B\)中的矩阵乘法需要进行精心设计,否则会花费很长时间。Google 解决这个问题的方法之一,就是使用强大的计算工具:MapReduce。将乘法运算拆分成若干任务,在不同节点进行并行运算,使得我们能在几乎瞬间得到搜索结果。
从 Power Method 看 PageRank
在前面的介绍中,Power Method 是实现特征分解的数值算法。但如果从另一个角度看,PageRank 或许就是在 Power Method 的思路上构建的。
还是刚才的例子,搜索关键词对应 5 个页面(图 10.2),如果 5 个页面还没有被排序,意味着我们点击每个页面的概率都是\(\frac{1}{5}\)(\(p_1=(\frac{1}{5},\frac{1}{5},\frac{1}{5},\frac{1}{5},\frac{1}{5})\))。进入网页后,我们又会随机点击页面中的链接,假设第一次进入的是页面3,那第二次点击后又有 \(\frac{1}{2}\)的概率进入页面1,\(\frac{1}{2}\)的概率进入页面 4。可以得到,经过两次点击后,停留在五个页面的概率分别为 \(p_2=p_1\mathbf{B}\),三次点击后,概率变为 \(p_3=p_2\mathbf{B}\),以此类推。如果进行无限多次点击,以更大概率停留的网页会更加重要:即通过 \(\lim\limits_{k\rightarrow\infty}p_k\) 对页面进行排序。
上面所述,实际上就是 Power Method 的实现过程。
仔细想,“最终停留在各页面的概率”这个概念似曾相识。这可以看作是马尔科夫链中的平稳概率分布。而转移概率矩阵,正是归一化后的邻接矩阵 \(\mathbf{B}\)。
其实不止搜索引擎的页面排序,其他问题中也用到了这样的思路:如在网络分析中(比如经济研究中的投入产出网络),各节点的重要性就可以用类似的特征向量描述。
来源:https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors↩︎