第 8 章马尔科夫链蒙特卡洛抽样

Monte Carlo方法，通常可追溯到1940年代后期的冯诺依曼在曼哈顿计划中的应用。第一个MCMC算法与另一台名为MANIAC的计算机相关，该计算机是在1952年初在Metropolis的指挥下在洛斯阿拉莫斯实验室建造。以当时项目参与人物理学家和数学家Metropolis命名的Metropolis算法一直被使用到如今。

Metropolis算法后来Hastings在1970年Metropolis算法后来被推广和扩展，形成了Metroplis-Hastings算法。Hastings和他的学生Peskun于1973年，1981年把该算法推广作为作为一般的统计模拟工具。

统计物理中使用的具有里程碑意义的吉布斯抽样由Geman兄弟于1984的论文进入统计应用领域。Gibbs名字来自物理学家威拉德·吉布斯（Willard Gibbs，1839–1903年）。

Gelfand和Smith在1990年的一篇论文大量使用了MCMC方法，之后激发了新的贝叶斯方法，统计计算中使用Gibbs抽样和Metropolis-Hastings算法。有趣的是，Tanner和Wong（1987）的论文与Gelfand和Smith（1990）的论文，证明从条件分布模拟就足够模拟联合分布渐近分布。这在理论上证明了MCMC方法的科学性。至此以后，MCMC方法得到了蓬勃发展，已经成为机器学习，统计计算中最为核心的计算工具之一。

8.1 介绍

在章节_7.3.2中的拒绝抽样算法需要有一个合理的猜想概率密度 \(g(x)\)，如图₈所示，如果 \(g(x)\) 与目标概率密度 \(f(x)\) 相差较远，拒绝抽样可能会效率很低甚至无法收敛。马尔科夫链蒙特卡洛（Markov chain Monte Carlo，MCMC）模拟则可以通过一个可适应性的猜想概率密度，也就是在每一步抽样中通过调整猜想概率使其尽可能的靠近目标概率密度。

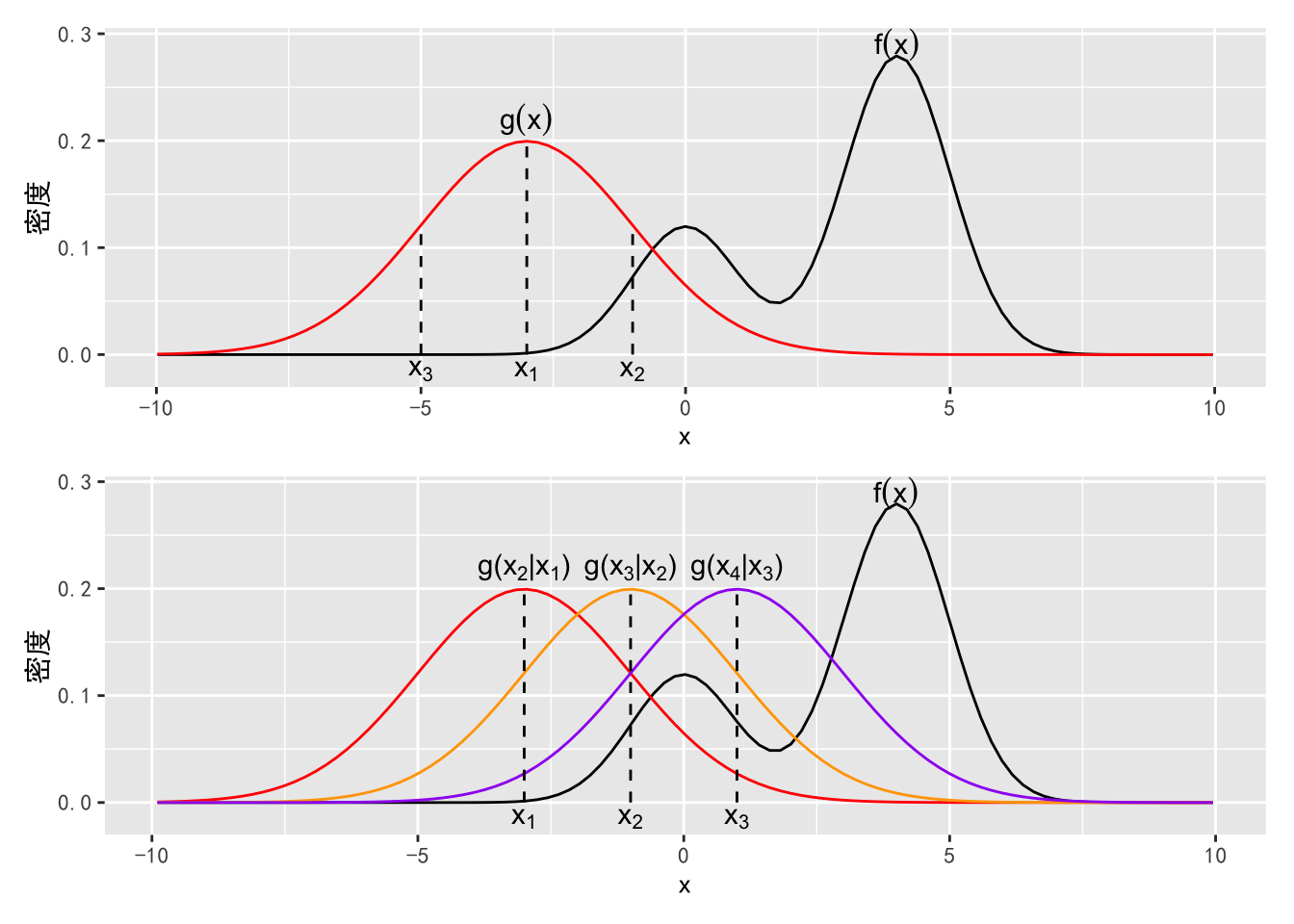
图8.1: 上：以 \(g(x)\) 为猜想概率密度对 \(f(x)\) 进行拒绝抽样；下：MCMC抽样

最常用的 MCMC 抽样算法包括 Metropolis-Hastings 算法和 Gibbs 抽样算法。

8.2 马尔科夫链

马尔科夫链（Markov chain）是一个随机变量序列 \(X_1, X_2, \cdots\)，对于任意时刻 \(t\)，给定 \(X_1, X_2, \cdots, x=X_{t-1}\) 的条件下， \(X_t\) 的分布只依赖于上一步的状态 \(X_{t-1}\)。

8.3 Metropolis-Hastings

假设我们想从 \(f(x)\) 中抽样，抽样的初始值为 \(x_0\)， Metropolis-Hastings 算法假设给定第 \(t-1\) 步的抽样 \(x_{t-1}\) 的条件下，\(x_t\) 的抽样由一个可以产生 \(x^*\) 的猜想概率密度和接受概率 \(\alpha\) 决定。其中 \(\alpha\) 就是接受 \(x^*\) 为下一状态的概率。具体来讲，Metropolis-Hastings 算法如下。

Metropolis-Hastings 算法

从 \(g(x^*|x_{t-1})\) 中抽取随机数 \(x^*\)。
计算接受概率

\[\alpha = \min\left(1, \frac{f(x^*)g(x_{t-1}|x^*)}{f(x_{t-1)}g(x^*|x_{t-1}))}\right).\]

产生均匀分布的随机数 \(U \sim U(0,1)\)，如果 \(U \leq \alpha\)，接受 \(x^*\)，即以 \(\alpha\) 为接受概率接受 \(x^*\)。若接受，\(x_t = x^*\)，否则 \(x_t = x_{t-1}\)。

8.3.1 随机游走 Metropolis-Hastings

在随机游走 Metropolis-Hastings 中， \(g(x^*|x_{t-1})\) 定义成 \(x^* = x_{t-1} + \epsilon\)，其中 \(\epsilon\) 服从一个以 0 为中心的对称分布 \(q\)，那么我们有\[g(x^*|x_{t-1}) = q(\epsilon),\] 并且 \[g(x_{t-1}|x^*) = q(-\epsilon) = q(\epsilon).\]此时因为 \(g(x^*|x_{t-1}) = g(x_{t-1}|x^*)\)，Metropolis-Hastings 算法中的接受概率 \(\alpha\) 就变成了 \[\alpha = \min\left(1, \frac{f(x^*)}{f(x_{t-1})}\right).\] 具体来讲，随机游走 Metropolis-Hastings 算法¹如下。

随机游走 Metropolis-Hastings 算法

从 (q) 中抽取 ()，其中 (q) 是一个以 0为中心的对称分布。让 (x^* = x_{t-1} + )。
计算接受概率

[= (1, ).]
产生均匀分布的随机数 (U U(0,1))，如果 (U )，接受(x^)，即以 () 为接受概率接受(x^)。若接受，(x_t = x^*)，否则 (x_t = x_{t-1})。

例3.1 从混合正态分布 \(f \sim 0.3 * N(0, 1) + 0.7 * N(4, 1)\) 中抽样。

随机游走 Metropolis-Hastings 的一个例子是假设 \(x^* \sim N(x_{t-1}, \sigma^2)\)。首先我们先画一下目标概率密度。

f <- function(x) {
    0.3 * dnorm(x, 0, 1) + 0.7 * dnorm(x, 4, 1)
}
ggplot(data.frame(x=runif(1000, -5, 8)), aes(x)) +
  stat_function(fun = f) +
  ylab('f(x)')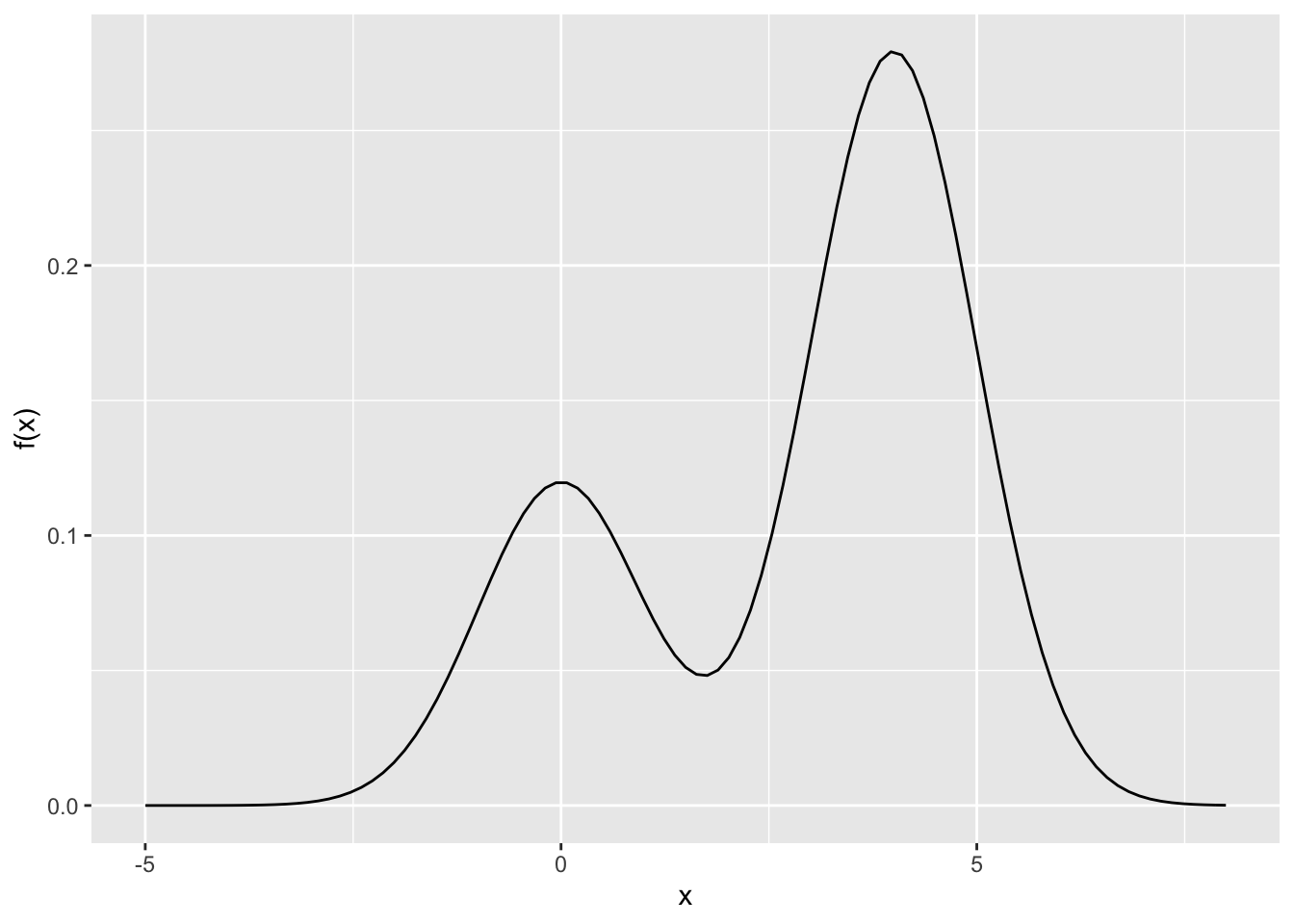

图8.2: 混合正态分布的概率密度图

接下来我们写出猜想概率密度函数。假设 \(\sigma = 4\)，即 \(x^* \sim N(x_{t-1}, 16)\)。

g <- function(x) rnorm(1, x, 4)

然后随机游走 Metropolis-Hastings 可以通过以下函数来实现。

rw.mh <- function(x0, f, g, n.steps = 1000, ...){
  x <- x0
  samples <- matrix(NA, n.steps, length(x))
  for (i in seq_len(n.steps)){
    # 猜想
    x.new <- g(x)
    # 计算接受概率
    alpha <- min(1, f(x.new, ...) / f(x, ...))
    # 判断是否接受
    if (runif(1) < alpha){
      x <- x.new
    }
    samples[i,] <- x
  }
  return(samples)
}

对于 \(f \sim 0.3 * N(0, 1) + 0.7 * N(4, 1)\) 的抽样为：

x0 <- 1
n.steps <- 2000
samples <- rw.mh(x0, f, g, n.steps = n.steps)

我们可以看到抽样的直方图是否接近于图_8.2中所示的密度图。

hist(samples, prob =TRUE)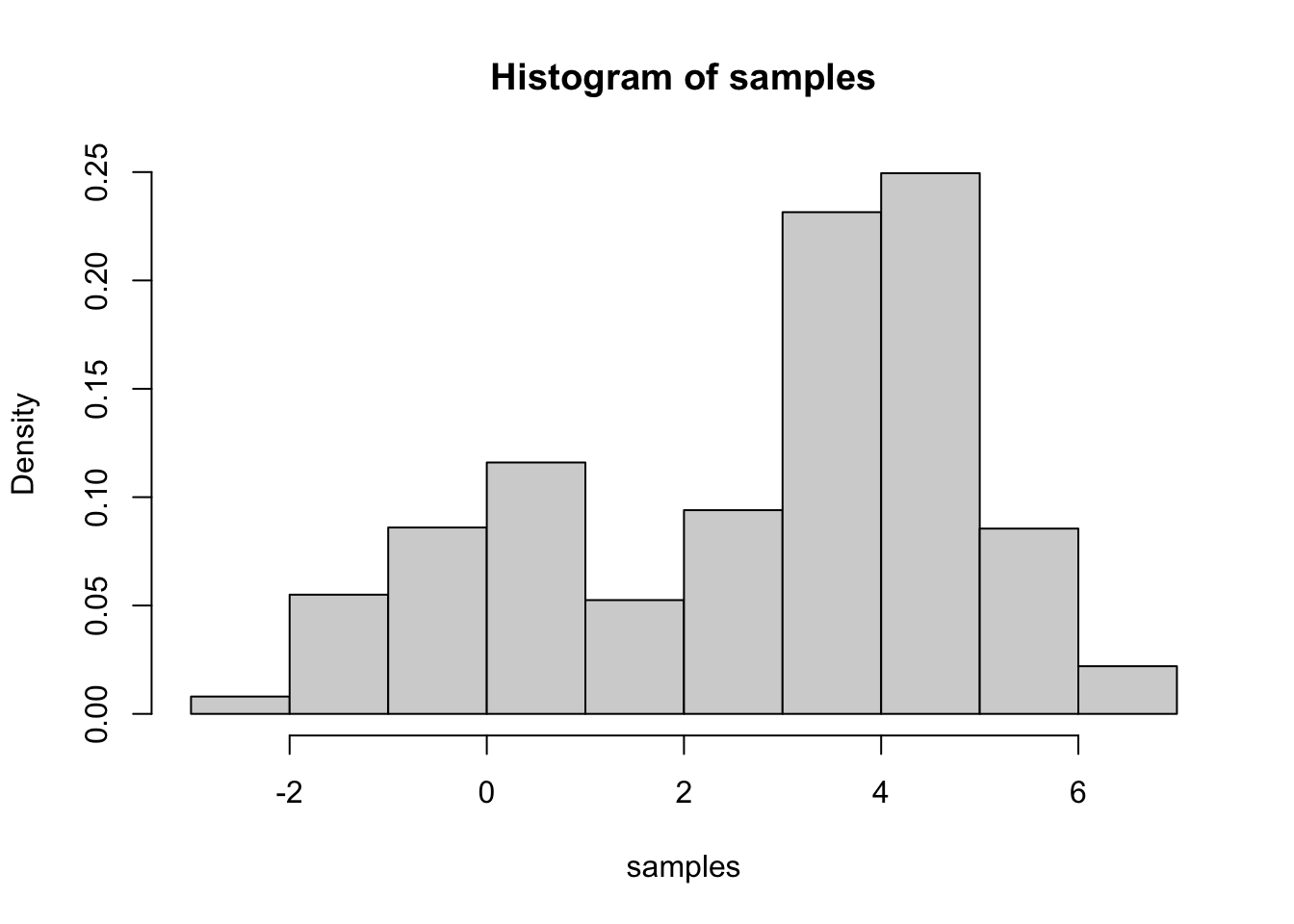

我们还可以画出抽样的路径图（trace plot）。

qplot(1:n.steps, samples, geom = "line", xlab = "迭代次数",
      ylab = "抽样") +
  theme(text = element_text(family = "STSong"))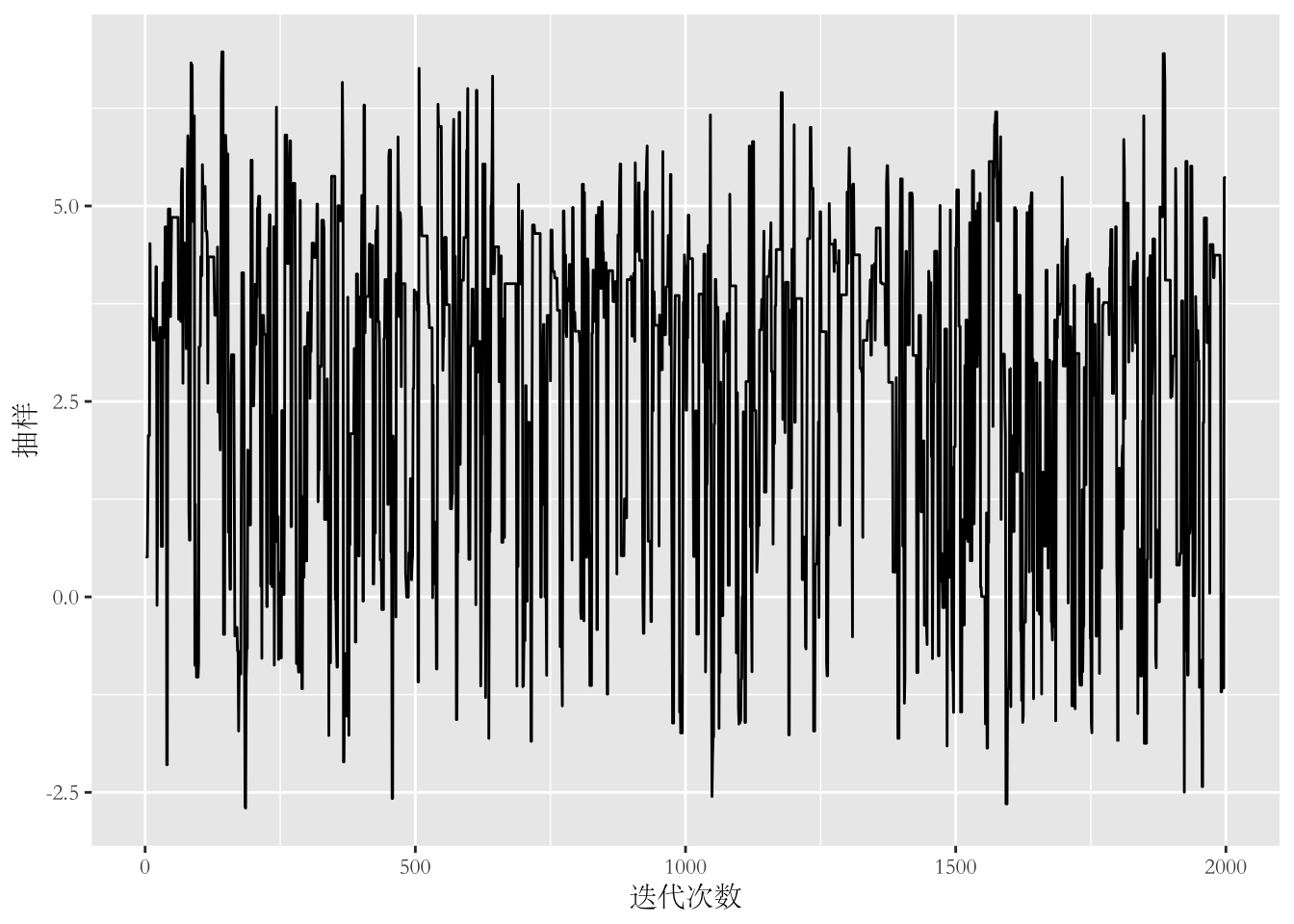

例2.2 从均值为 \(\mu = (\mu_1, \mu_2)\)，协方差阵为 \(\Sigma=\left(\begin{array}{cc}\sigma_{1}^{2} & \rho \\ \rho & \sigma_{2}^{2}\end{array}\right)\) 的二元正态分布中抽样。

一个 \(p\) 元正态分布的密度函数为\[f_{X_1,X_2, \cdots, X_p}(x_1, x_2, \cdots, x_p) = \frac{1}{2\pi \sqrt{|\Sigma|}}\exp\left(-\frac{1}{2}(\mathbf{x}-\mu)^T\Sigma^{-1}(\mathbf{x}-\mu)\right).\]

首先写出二元正态分布的概率密度函数 \(f_{X,Y}(x, y)\) 并画出其等高线图。

f <- function(x,
              mu = c(-1, 1),
              Sigma = matrix(c(1, .25, .25, 1.5), 2, 2)){
  logdet <- as.numeric(determinant(Sigma, TRUE)$modulus)
  cons <- length(mu) * log(2 * pi) + logdet
  Sigma.i <- solve(Sigma)
  dx <- x - mu
  exp(-(cons + rowSums((dx %*% Sigma.i) * dx))/2)
}
x <- seq(-4, 1.5, length = 100)
y <- seq(-2, 4, length = 100)
xy <- expand.grid(x = x, y = y)
z <- matrix(apply(as.matrix(xy), 1, f), length(x), length(y))
image(x, y, z, las = 1)
contour(x, y, z, add = TRUE)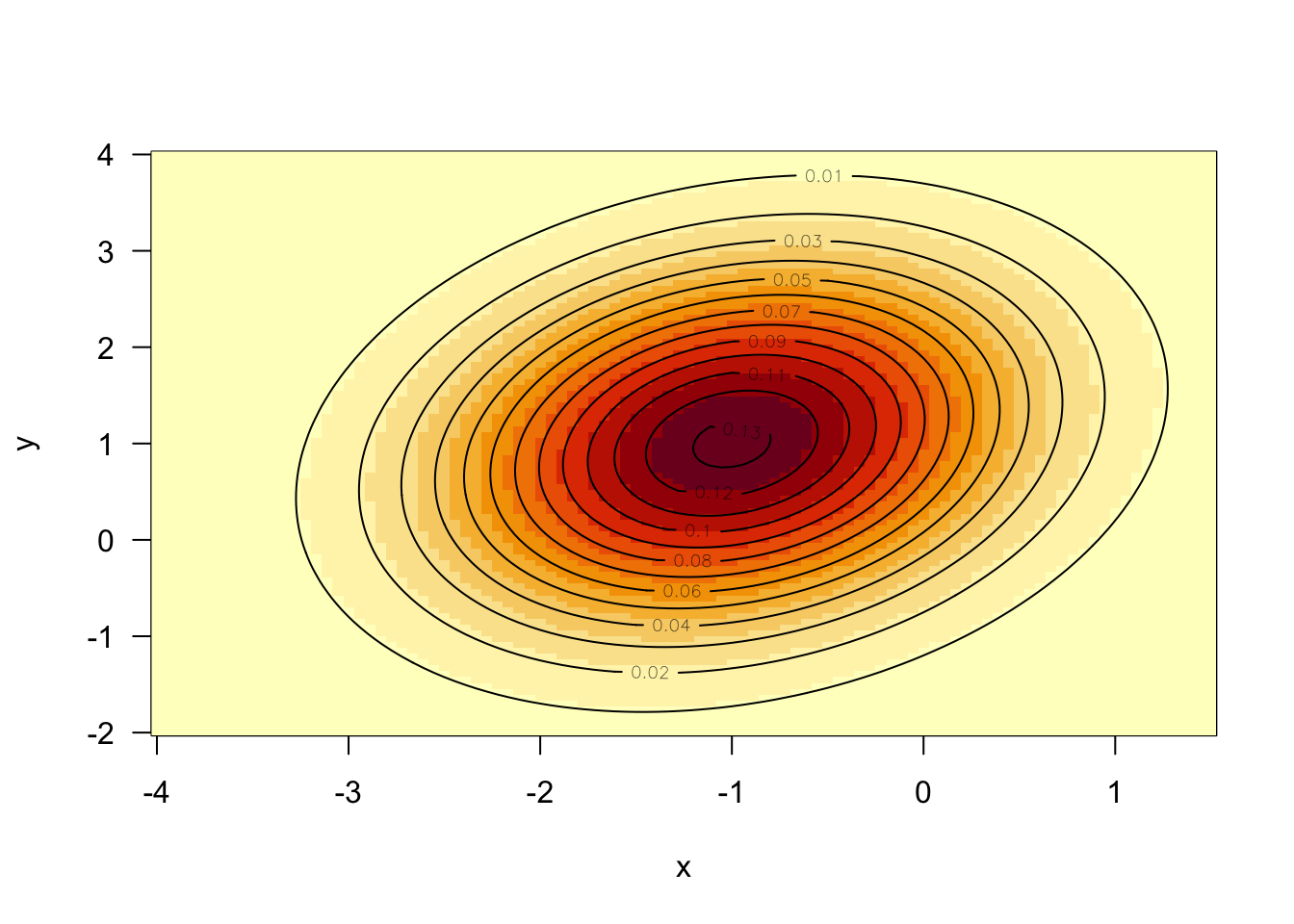

基于随机游走 Metropolis-Hastings，每一步的猜想概率密度可以定义为

g <- function(x, d = 2){
    x + runif(length(x), -d/2, d/2)
}

然后基于 Metropolis-Hastings 进行抽样，画出抽样的密度及二元正态分布的等高线图。

set.seed(Sys.Date())
samples <- rw.mh(c(-4, 4), f, g, 10000)
smoothScatter(samples, xlab ='x', ylab = 'y')
contour(x, y, z, add = TRUE)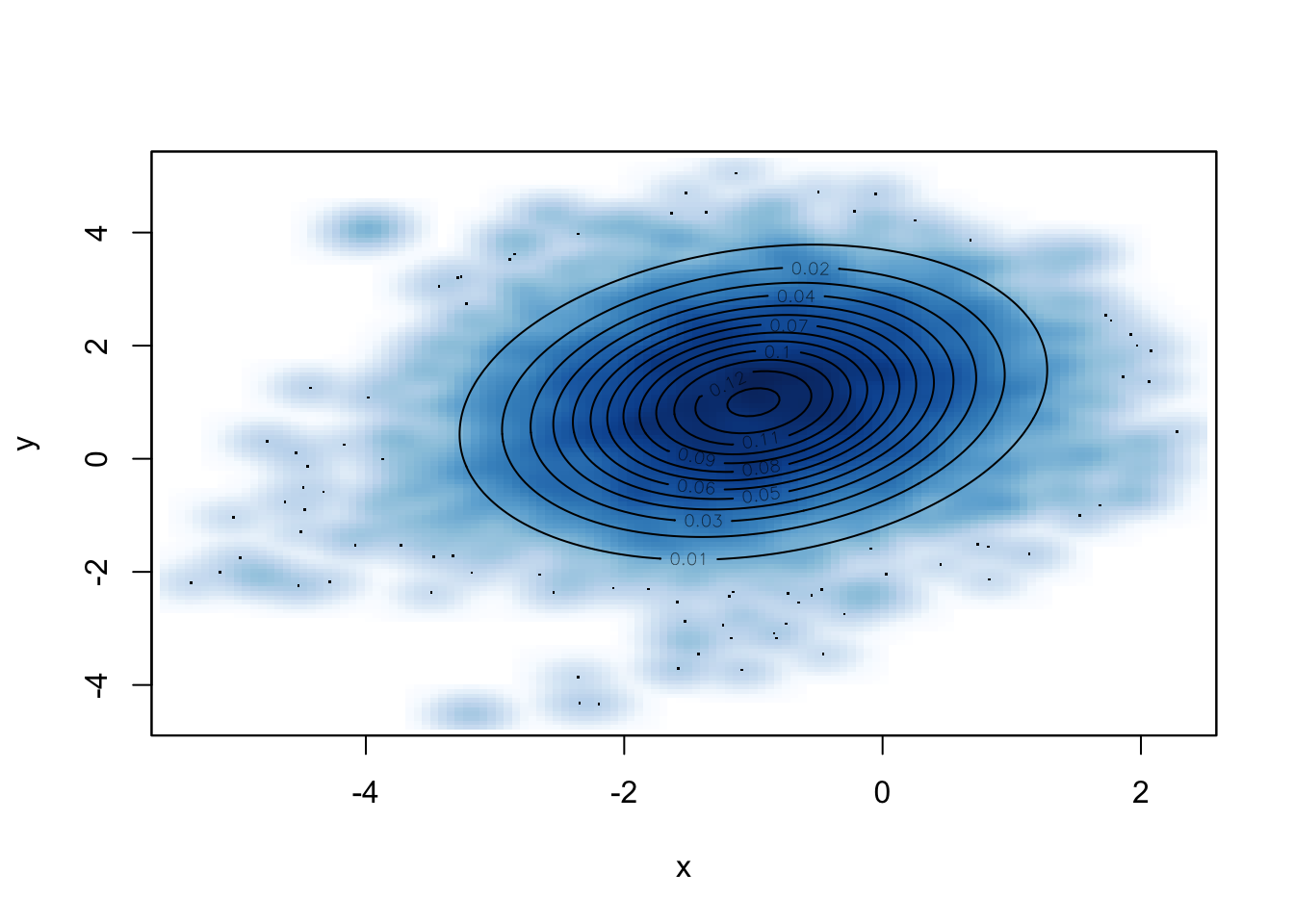

8.3.2 独立 Metropolis-Hastings

在独立 Metropolis-Hastings 中，\(g(x^*|x_{t-1}) = g(x^*)\)，也就是说猜想概率密度不依赖于上一步的状态 \(x_{t-1}\)，那么独立 Metropolis-Hastings 如下。

独立 Metropolis-Hastings 算法

从 (q) 中抽取 ()，其中 (q) 是一个以 0为中心的对称分布。让 (x^* = x_{t-1} + )。
计算接受概率

[= (1, ).]
产生均匀分布的随机数 (U U(0,1))，如果 (U )，接受(x^)，即以 () 为接受概率接受(x^)。若接受，(x_t = x^*)，否则 (x_t = x_{t-1})。

8.4 Gibbs 抽样

在多维问题中，Metropolis-Hastings 算法每一次更新的是一个多维向量，所以一个 \(p\) 维问题就需要一个 \(p\) 维的猜想概率密度，Gibbs 抽样则可以把多维问题分解为简单的一维问题。

假设我们要从二元密度 \(f(x,y)\) 中抽样，且我们有全部的条件分布 \(f(x|y)\) 和 \(f(y|x)\)，那么我们可以通过 Gibbs 抽样算法按照以下步骤进行抽样。

Gibbs 抽样算法

假设当前状态为 \((x_i ,y_i)\)，重复以下过程直到得到目标数量的样本。

从 (f(x|y_i)) 中抽取 (x_{i+1})。
从 (f(y|x_{i+1})) 中抽取 (y_{i+1})。

在 Gibbs 抽样中，在每一步条件概率密度的抽样中都用了其他变量的最近状态。Gibbs 抽样中的 \(x\) 和 \(y\) 可以互换位置，而且适用于 \(p > 2\) 的情况。例如，当 \(p = 3\) 时，如果要从 \(f(x, y, z)\) 中抽样，假设当前状态为 \((x_i ,y_i, z_i)\)，Gibbs 抽样重复以下过程：

从 \(f(x|y_i, z_i)\) 中抽取 \(x_{i+1}\)。
从 \(f(y|x_i, z_i)\) 中抽取 \(y_{i+1}\)。
从 \(f(z|x_i, y_i)\) 中抽取 \(z_{i+1}\)。

例2.5 从均值为 \(\mu = (\mu_1, \mu_2)\)，协方差阵为 \(\Sigma=\left(\begin{array}{cc}\sigma_{1}^{2} & \rho \\ \rho & \sigma_{2}^{2}\end{array}\right)\) 的二元正态分布中进行 Gibbs 抽样。

基于 Gibbs 抽样，假设当前状态为 \((x_i ,y_i)\)，重复以下过程直到得到目标数量的样本。

从 \(f(x|y_i) \sim N(\mu_1 + \rho \frac{\sigma_1}{\sigma_2}(y_i-\mu_2), \sigma_1^2(1-\rho))\) 中抽取 \(x_{i+1}\)。
从 \(f(y|x_{i+1}) \sim N(\mu_2 + \rho \frac{\sigma_2}{\sigma_1}(x_{i+1} -\mu_1), \sigma_2^2(1-\rho))\) 中抽取 \(y_{i+1}\)。

gibbs <- function(x0, mu, Sigma, n.steps = 1000){
  mu1 <- mu[1]
  mu2 <- mu[2]
  sigma1 <- Sigma[1, 1]
  sigma2 <- Sigma[2, 2]
  rho <- Sigma[1, 2]
  samples <- matrix(NA, n.steps, 2)
  samples[1,1] <- x <- x0[1]
  samples[1,2] <- y <- x0[2]

  for (i in 1:n.steps-1) {
    samples[i+1, 1] <- x <-
      rnorm(1, mu1 +
              rho * sigma1 * (y-mu2) /
              sigma2, sqrt((sigma1^2) * (1 - rho^2) ))
    samples[i+1, 2] <- y <-
      rnorm(1, mu2 +
              rho * sigma2 * (x-mu1) /
              sigma1, sqrt((sigma2^2) * (1 - rho^2) ))
  }
  return(samples)
}
set.seed(Sys.Date())
mu = c(-1, 1)
Sigma = matrix(c(1, .25, .25, 1.5), 2, 2)
samples <- gibbs(c(-4,4), mu, Sigma, 10000)
smoothScatter(samples, xlab ='x', ylab = 'y')
contour(x, y, z, add = TRUE)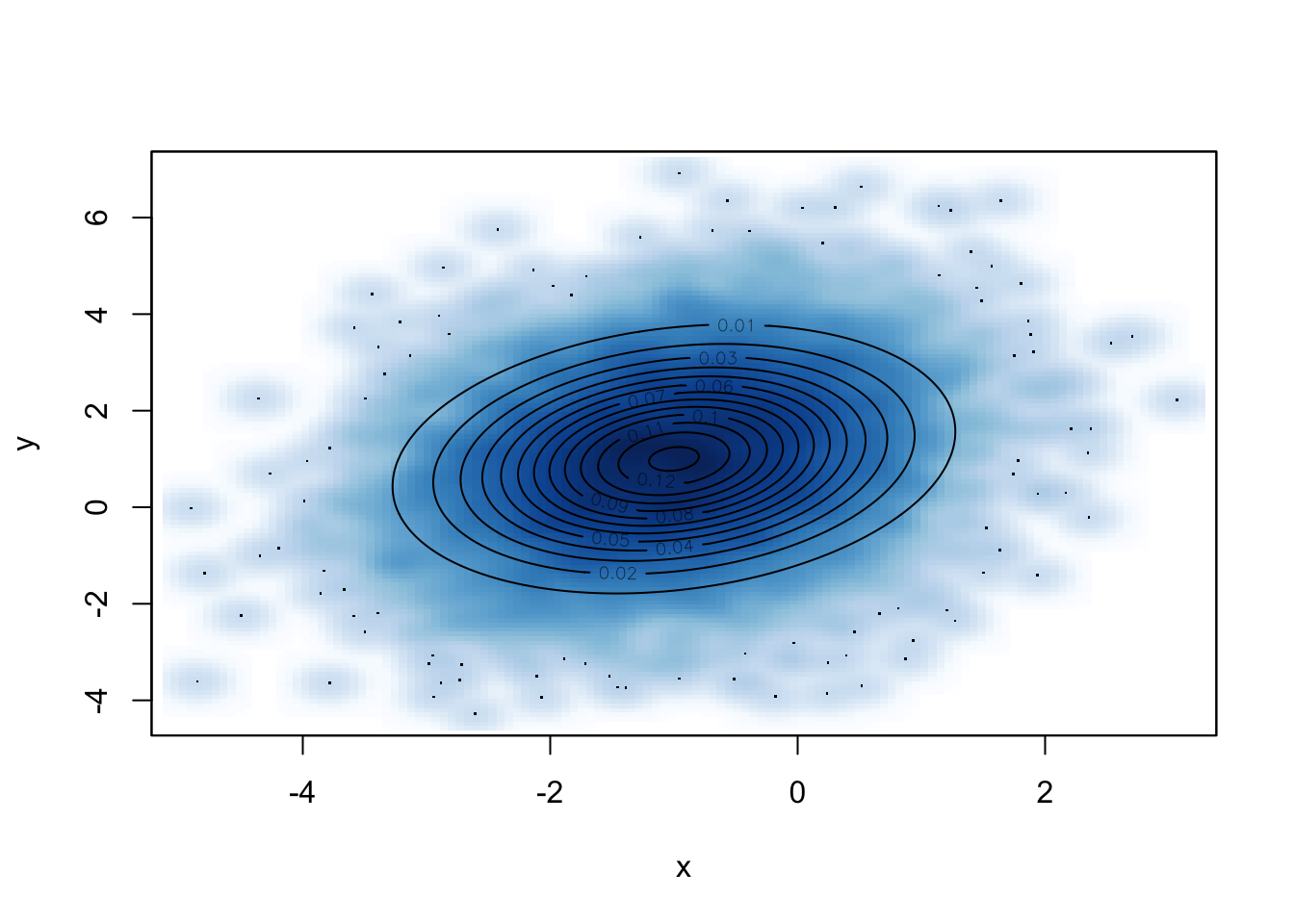

8.5 Gibbs 抽样与 Metropolis-Hastings 算法的关系

在 Gibbs 抽样中每一步的猜想概率密度为条件概率，我们可以计算接受概率 \(\alpha\):\[\begin{aligned} \alpha &= \mathrm{min} \left(1, \frac{p\left(x_{i+1}, y\right) p\left(x_{i} | y\right)}{p\left(x_{i}, y\right) p\left(x_{i+1} | y\right)}\right) \\ &= \mathrm{min} \left(1, \frac{p(x_{i+1} | y) p(y) p\left(x_{i} | y\right)}{p(x_{i}| y) p(y) p(x_{i+1} | y)}\right) \\ &=1.\end{aligned}\]这也就是说，Gibbs 抽样其实是以条件概率密度为猜想概率密度的 Metropolis-Hastings，在每一步的接受概率为 1。

8.6 MCMC 的收敛效率

在例6.1中，如果我们增大或减小 \(\sigma\) ，会得到什么样的结论呢？我们分别画出 \(\sigma = 4\)，\(\sigma = 50\) 以及 \(\sigma = 0.1\) 的路径图。

# 定义不同的猜想概率
g1 <- function(x) rnorm(1, x, 0.1)
g2 <- function(x) rnorm(1, x, 4)
g3 <- function(x) rnorm(1, x, 50)

# 分别抽样
set.seed(Sys.Date())
samples1 <- rw.mh(-5, f, g1, n.steps)
samples2 <- rw.mh(-5, f, g2, n.steps)
samples3 <- rw.mh(-5, f, g3, n.steps)

# 画出路径图
samples <- data.frame(iter = 1:n.steps, samples1 = samples1,
                      samples2 = samples2, samples3 = samples3)
cggplot(samples, aes(iter)) +
  geom_line(aes(y = samples1, colour = "sd = 0.1")) +
  geom_line(aes(y = samples2, colour = "sd = 4")) +
  geom_line(aes(y = samples3, colour = "sd = 50")) +
  scale_colour_discrete(expression(sigma),
                        labels = c('0.1', '4', '50')) +
  xlab('迭代次数') + ylab('抽样')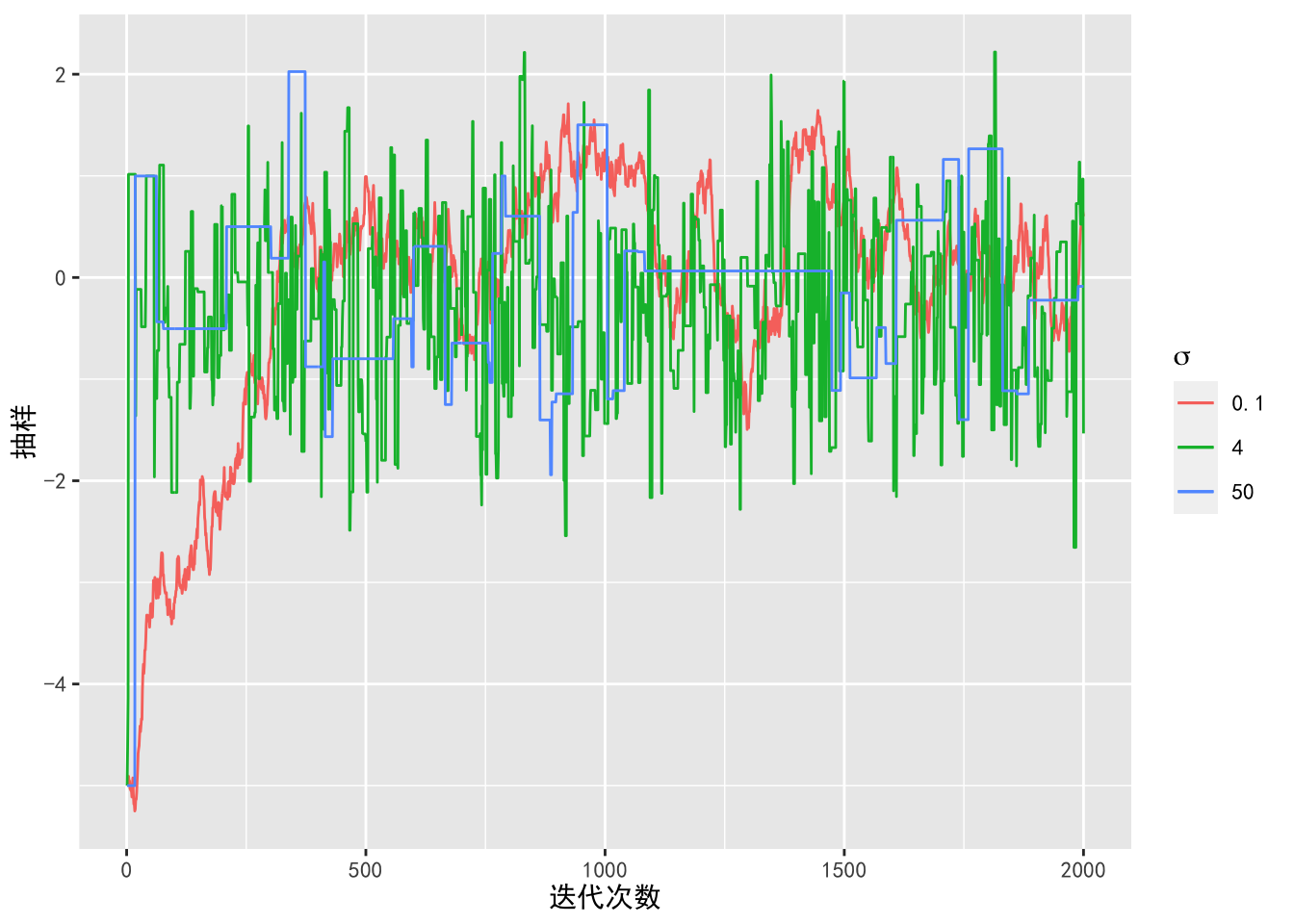

图8.3: 不同的猜想概率密度标准差下混合正态分布的抽样

不同的标准差设定下的抽样直方图如下。

library(reshape2)
library(dplyr)
samples.melt <- data.frame(iter = 1:n.steps,
                           samples1 = samples1,
                           samples2 = samples2,
                           samples3 = samples3) %>%
  select(-iter) %>% melt()
cggplot(samples.melt,aes(x=value, color=variable)) +
  geom_density(alpha=0.25, size = 1.3) +
  scale_color_discrete(expression(sigma),
                       labels = c('0.1', '4', '50')) +
  xlab('x') + ylab('密度')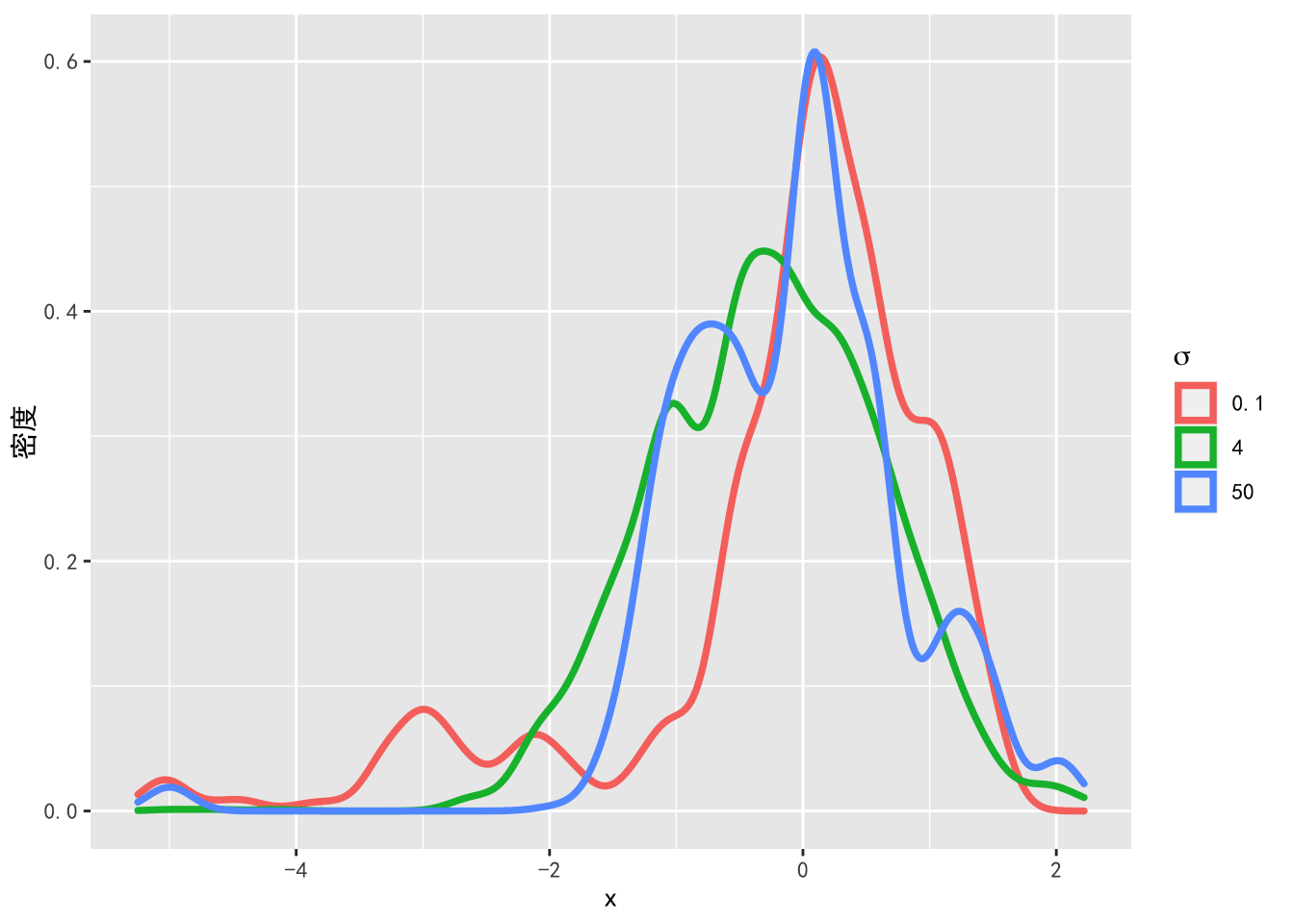

图8.4: 不同的猜想概率密度标准差下混合正态分布的抽样密度图

由图_8.3可以看出，当 \(\sigma = 50\) 时，Metropolis 算法的抽样过程中有很多样本被拒绝，导致算法的接受率很低。当 \(\sigma = 0.1\) 时，算法的接受率几乎为 \(100\%\)，但这也不是一个好的猜想概率密度，由图_8.4可以看出，\(\sigma = 0.1\) 对应的抽样密度离目标概率密度较远，因为猜想概率密度的标准差很小，所以无法抽到尾部的样本。这时如果增加抽样次数，马尔科夫链将收敛于目标概率密度，但导致算法的效率很低。

8.6.1 蒙特卡洛误差

有了 \(f(x)\) 的随机样本 \(x_1, x_2, \cdots, x_M\)，我们就可以计算相关的汇总统计量，比如我们可以计算它们的均值用来估计 \(E_X\)：

\[E_X \approx \frac{1}{M}\sum\limits_{i = 1}^M x_i.\]因为我们用样本均值进行估计 \(E_X\)，所以会导致估计误差，这个误差会随着抽样数量的增加而减小。我们把这个误差称作蒙特卡洛误差（Monte Carlo Error）。一种测量蒙特卡洛误差的方法是计算样本均值的方差，即

\[ \begin{aligned} \operatorname{Var}\left(\frac{1}{M} \sum_{i=1}^{M} x_i\right) &=\frac{1}{M^{2}} \operatorname{Var}\left(\sum_{i=1}^{M} x_i\right) \\ &=\frac{1}{M^{2}} \sum_{i=1}^{M} \operatorname{Var}\left(x_i\right)+\frac{2}{M^{2}} \sum_{i=1}^{M} \sum_{j>i} \operatorname{cov}\left(x_i, x_j\right) \\ &=\frac{\operatorname{Var}(X)}{M}+\frac{2}{M^{2}} \sum_{i=1}^{M} \sum_{j>i} \operatorname{cov}\left(x_i, x_j\right) \end{aligned}. \]由此可见，在马尔科夫链中样本之间相关性越小，样本均值的方差越小。图_8.5展示了例6.1中不同的猜想概率密度标准差下抽取样本的自相关图。当 \(\sigma = 4\) 时，样本之间的自相关最小，这时蒙特卡洛误差最小。

ggcor <- function(x){
  bacf <- acf(x, plot = FALSE)
  bacfdf <- with(bacf, data.frame(lag, acf))
  p <- ggplot(data = bacfdf,
              mapping = aes(x = lag, y = acf)) +
    geom_hline(aes(yintercept = 0)) +
    geom_segment(mapping = aes(xend = lag, yend = 0))
  return(p)
}

p1 <- ggcor(samples1) + ggtitle(bquote(sigma ~ "= 0.1"))
p2 <- ggcor(samples2) + ggtitle(bquote(sigma ~ "= 4"))
p3 <- ggcor(samples3) + ggtitle(bquote(sigma ~ "= 50"))
library(patchwork)
p1 / p2 / p3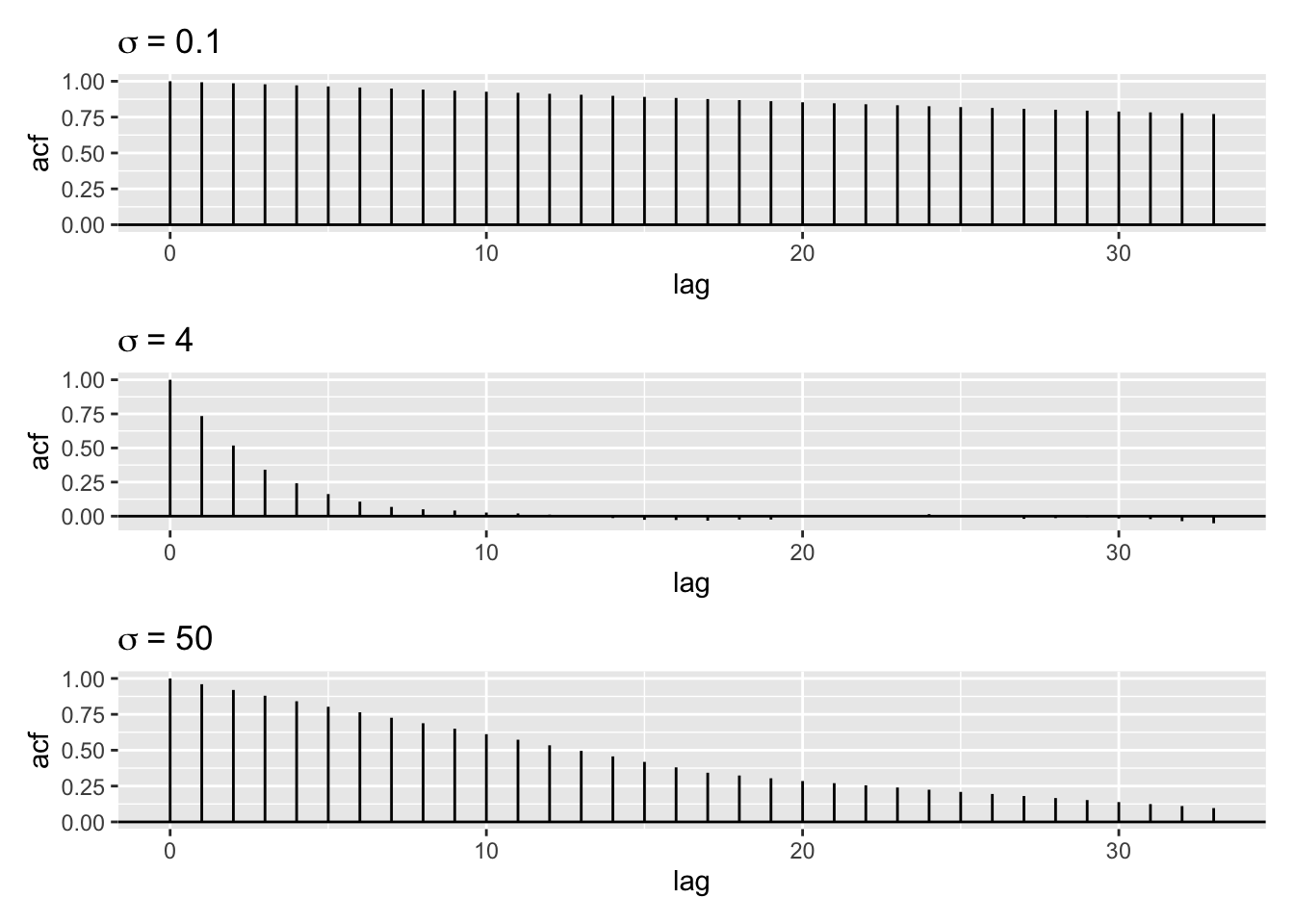

图8.5: 不同的猜想概率密度标准差下混合正态分布的抽样自相关图

8.6.2 有效样本量

有效样本量（Effective Sample Size，ESS）通常被用来比较不同的猜想概率密度，我们用 \(M_{\operatorname{ESS}}\) 表示有效样本量，它可以通过以下式子得到：

\[\operatorname{Var}\left(\frac{1}{M} \sum_{i=1}^{M} x_i\right) = \frac{\operatorname{Var}(X)}{M}+\frac{2}{M^{2}} \sum_{i=1}^{M} \sum_{j>i} \operatorname{cov}\left(x_i, x_j\right) = \frac{\operatorname{Var}(X)}{M_{\operatorname{ESS}}}.\]

在 R 中，\(M_{\operatorname{ESS}}\) 可以通过 R 包 coda 来计算。

coda::effectiveSize(samples1)
#>  var1 
#> 7.011
coda::effectiveSize(samples2)
#>  var1 
#> 338.4
coda::effectiveSize(samples3)
#>  var1 
#> 52.95

由此可见，不同的猜想概率密度标准差下的有效样本量差异较大。当 \(\sigma = 4\) 时，有效样本量最大。

8.7 基于优化的抽样算法

随机游走 Metropolis-Hastings 算法也就是最原始的 Metropolis 算法。↩︎

第 8 章 马尔科夫链蒙特卡洛抽样