第 2 章 求根算法

求根算法是数学和统计计算中的基本概念，它可以帮助我们找到一个方程的根。最早的求根方法之一是二分法，可以追溯到古希腊时期。其次是常用的牛顿法，我们在本书中将两种方法分别展开。

2.1 二分法

二分法是一种求根方法，也称为区间减半法，是求解非线性方程的最基本的方法之一。它的历史可以追溯到公元前5世纪的希腊数学家欧多克索斯。在数学史上，二分法被视为求根问题的第一个数值方法，也是最古老的数值方法之一。二分法的基本思想是将待求解区间不断二分，每次选择新的区间，使得方程在该区间内的函数值异号（即函数值经过零点），并将零点所在的新区间继续二分，直到找到满足精度要求的近似解。尽管二分法简单，但它在数值计算中有重要的应用。在实践中，二分法具有较高的可靠性和收敛速度，可以用于求解非线性方程，特别是实际问题中的一些复杂非线性方程。此外，二分法也可以用于优化问题的求解中，例如确定函数的最小值或最大值。除了在数学中应用外，二分法也在计算机科学中得到广泛应用。在搜索和排序算法中，二分法被广泛使用来查找元素或确定元素的位置。例如，在二分查找算法中，给定一个已排序的数组和一个目标值，算法通过比较目标值与数组中间元素的大小关系，每次将搜索范围缩小一半，直到找到目标值或搜索范围为空。

更具体的，二分法（Bisection Algorithm）是一种可以用来寻找一维连续函数 \(f(x)\) 的根 \(x_0\) 的算法，它的基本思想是从一个较大的包含根 \(x_0\) 的区间开始，逐步缩小区间直到收敛到 \(x_0\) 附近。该算法的理论基础是中值定理，即对于连续函数 \(f: [a,b]\rightarrow \mathbb{R}\)，且假设 \(f(a)<f(b)\)，若对任意数 \(u\) 满足 \(f(a)<u<f(b)\)，则存在一点 \(c,~(a < c < b)\)，使得 \(f(c) = u\)。

二分法

  1. 选择初始区间 \([a, b]\)，且 \(\text{sign}(f(a)) \neq \text{sign}(f(b))\)，

  2. 按照以下迭代过程进行迭代直到 \(|b-a|<\epsilon\) 或 \(|f(b) - f(a)|<\epsilon\)：

    1. 计算中点 \(c = \frac{a+b}{2}\)；
    2. 若 \(f(c) = 0\)，终止迭代；
    3. 若 \(\text{sign}(f(a)) \neq \text{sign}(f(c))\)，则 \(b \leftarrow c\)，否则 \(a\leftarrow c\)，返回第1步。

  3. 输出 \(c\)。

bisection.root <- function(f, a, b, tol = 1e-9, 
                           max.iter = 100){
  iter <- 0
  if (abs(f(a)) < tol) return(a)
  if (abs(f(b)) < tol) return(b)
  # 当初始区间两端同号时，认为没有根
  if (f(a) * f(b) > 0) return(NULL)
  
  # 迭代直到满足条件
  while((abs(b-a) > tol) && (iter < max.iter)) {
    middle_point <- (a + b) / 2
    iter <- iter + 1
    fc = f(middle_point)
    cat("迭代第", iter, "次，a =", a, "，b =", b, '\n')
    
    # 当中点的函数值很接近0时，认为该点为根
    if (abs(fc) < tol) return(middle_point)
    # 当中点与左端点的符号不同时，以中点为新的右端点进行查找
    if (fc * f(a) < 0){
      b <- middle_point
    } else {
      a <- middle_point
    }
  }
  return((b+a)/2)
}

例2.1 求 \(f(x) = x^2 - 5\) 的根

以\([-4, 0]\)作为初始区间，可以找到其中一个根约等于\(-2.236\)，将初始区间换成\([0,4]\)后可以找到另一个根约等于\(2.236\)。

f <- function(x){x^2 - 5}
roots <- bisection.root(f, 0, 4, tol = 1e-3)
#> 迭代第 1 次，a = 0 ，b = 4 
#> 迭代第 2 次，a = 2 ，b = 4 
#> 迭代第 3 次，a = 2 ，b = 3 
#> 迭代第 4 次，a = 2 ，b = 2.5 
#> 迭代第 5 次，a = 2 ，b = 2.25 
#> 迭代第 6 次，a = 2.125 ，b = 2.25 
#> 迭代第 7 次，a = 2.188 ，b = 2.25 
#> 迭代第 8 次，a = 2.219 ，b = 2.25 
#> 迭代第 9 次，a = 2.234 ，b = 2.25 
#> 迭代第 10 次，a = 2.234 ，b = 2.242 
#> 迭代第 11 次，a = 2.234 ，b = 2.238 
#> 迭代第 12 次，a = 2.234 ，b = 2.236

二分法的优点在于容易理解和实现，不需要知道函数 \(f(x)\) 的梯度之类的信息，它的缺点在于只适用于一维函数，并且相比于之后讲到的牛顿法等算法，收敛速度较慢。

特别地，二分法在以下几种情况中使用可能出现问题：

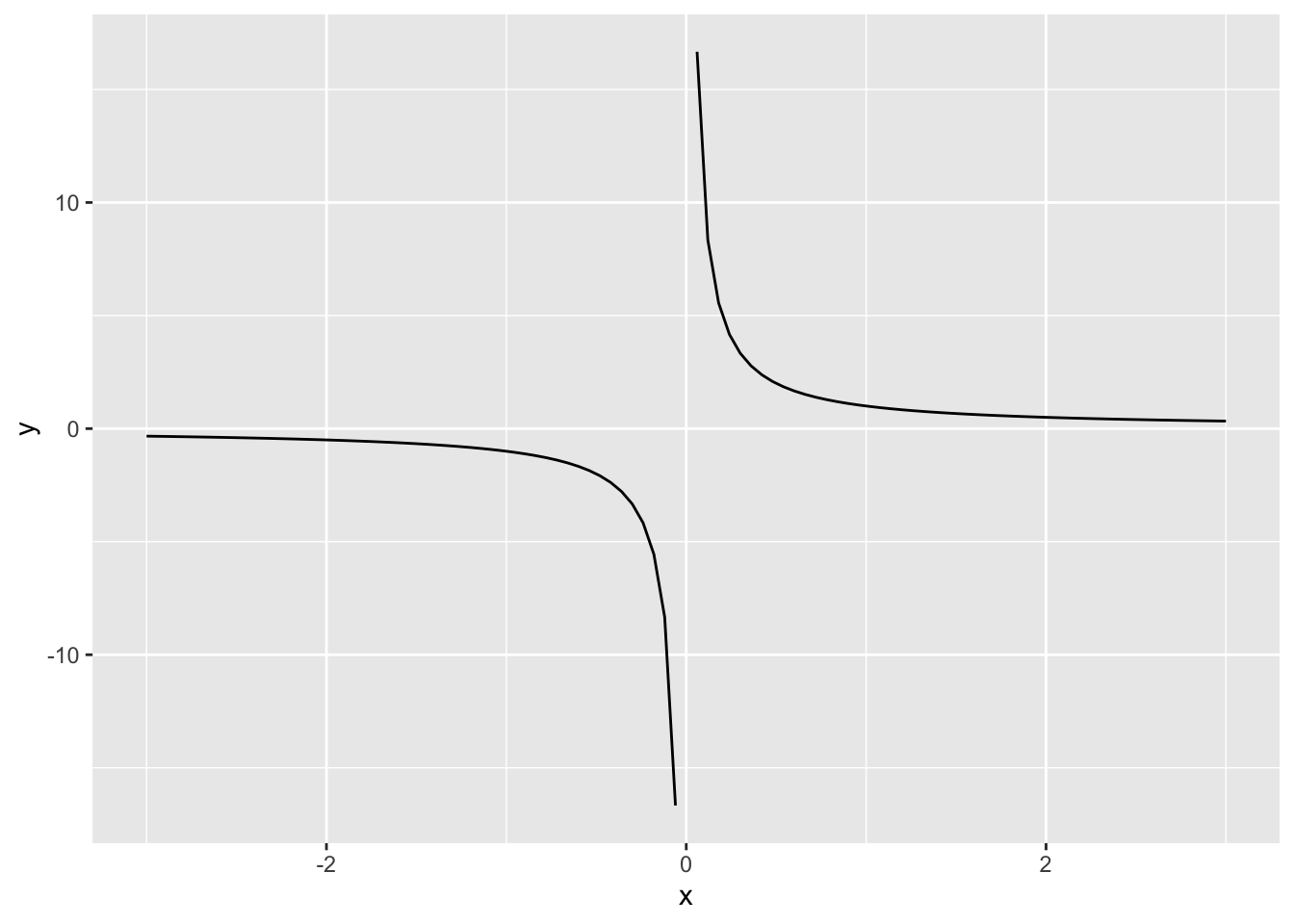
在这种情况下，若采用 \(|b-a|<\epsilon\) 作为终止条件，二分法可能错把不是根的点当做根。

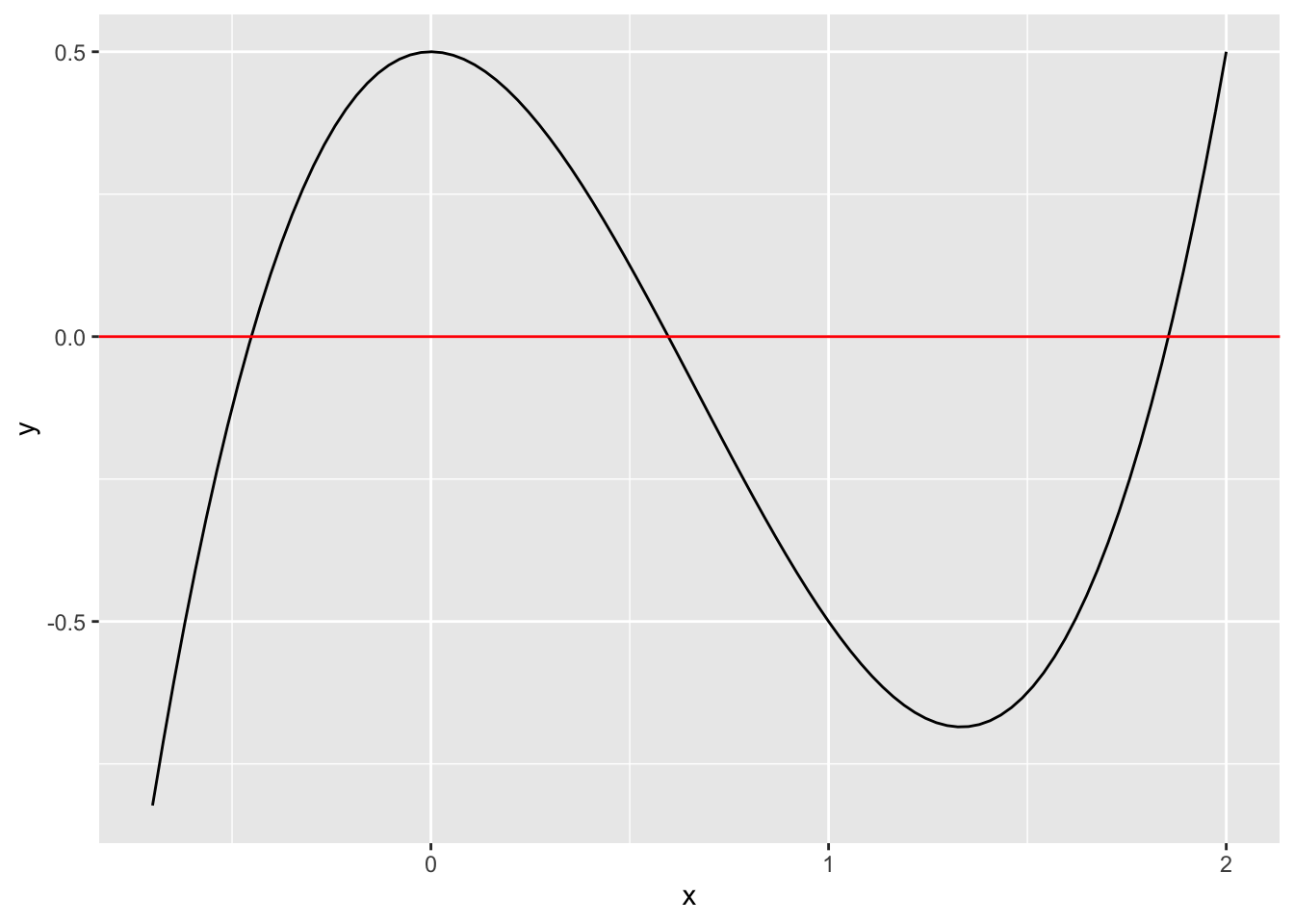当函数具有多个根时，需要调整左右端点来得到所有的根。

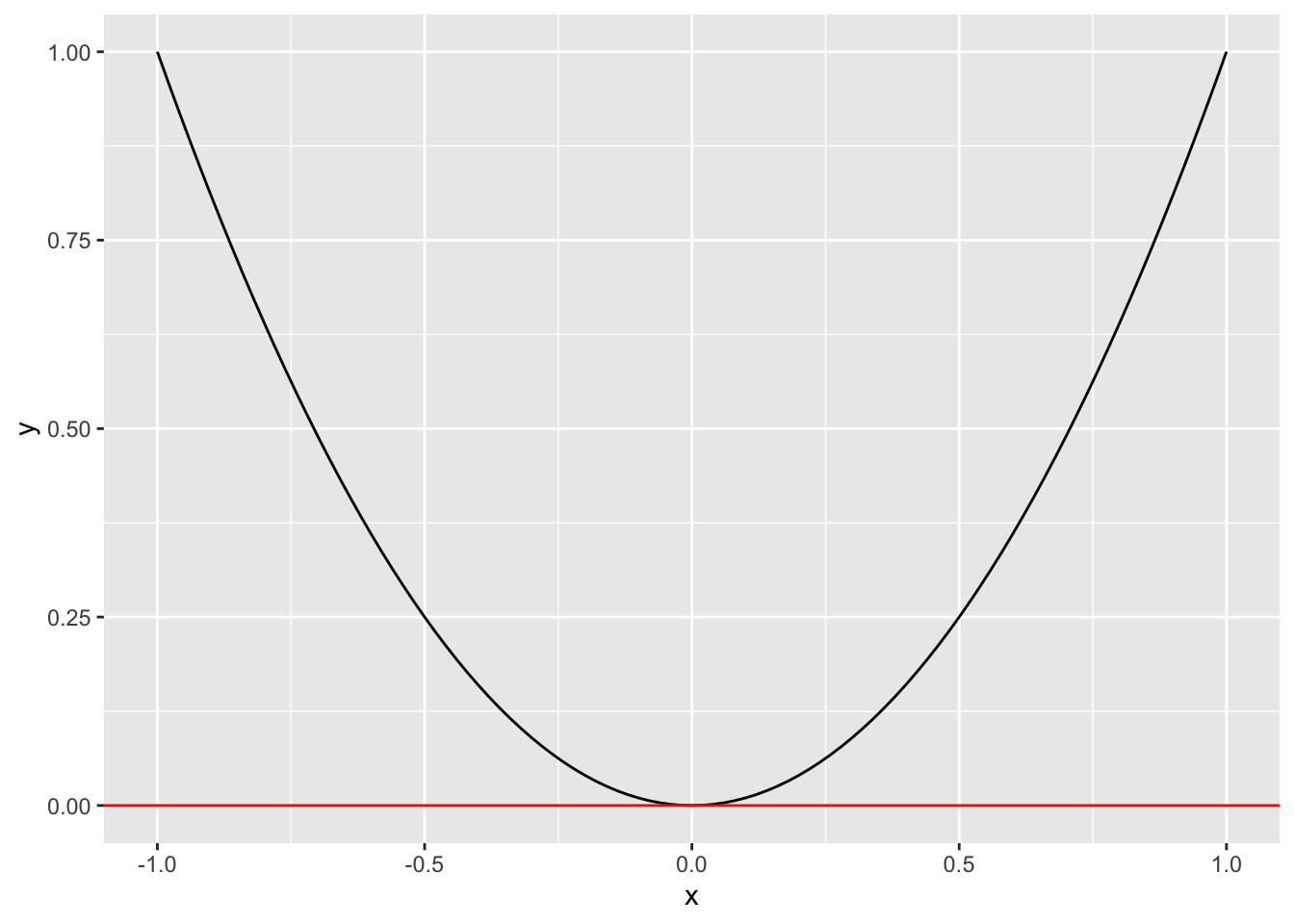上图中的函数 \(f(x)=x^2\) 无法找到 \([a,b]\) 使得 \(\text{sign}(f(a))\neq \text{sign}(f(b))\)，但该函数具有根 \(x=0\)。

2.2 收敛速度

比较不同算法的其中一种方式是比较它们的收敛速度（Rate of Convergence），例如对于迭代的最优化算法，收敛速度可以理解为该算法需要迭代多少步才可以达到最优点。在这里我们主要关注三种收敛速度：线性收敛（Linear Convergence）、超线性收敛（Superlinear Convergence）以及平方收敛（Quadratic Convergence），它们的相对速度由慢到快。

2.2.1 线性收敛

对于序列 \(\{x_n\}, x_n\rightarrow x_\infty\)，若存在 \(r \in (0, 1)\) 使得

\[ \lim\limits_{n\rightarrow \infty}\frac{|x_{n+1}-x_\infty|}{|x_n-x_\infty|} \leq r, \]则称序列 \(\{x_n\}\) 线性收敛。

例2.2 序列 \(x_n = 1 + (\frac{1}{2})^n\) 线性收敛。

\[ \frac{|x_{n+1} - x_{\infty}|}{|x_n - x_{\infty}|} = \frac{(\frac{1}{2})^{n+1}}{(\frac{1}{2})^n} = \frac{1}{2} \]该序列的收敛速度为 \(\frac{1}{2} \in (0, 1)\)。

2.2.2 超线性收敛

对于序列 \(\{x_n\}, x_n\rightarrow x_\infty\)，若

\[ \lim\limits_{n\rightarrow \infty}\frac{|x_{n+1}-x_\infty|}{|x_n-x_\infty|} = 0, \]则称序列 \(\{x_n\}\) 超线性收敛, 相比于线性收敛，超线性收敛的速度更快。线性收敛的序列永远不会收敛到最优值 \(x_\infty\)，而超线性收敛可以收敛到最优值。

例2.3 序列 \(x_n = 1 + (\frac{1}{n})^n\) 线性收敛。

\[ \lim_{n\rightarrow\infty}\frac{|x_{n+1} - x_{\infty}|}{|x_n - x_{\infty}|} = \frac{(\frac{1}{n+1})^{n+1}}{(\frac{1}{n})^n} = 0 \]该序列超线性收敛。

2.2.3 平方收敛

对于序列 \(\{x_n\}, x_n\rightarrow x_\infty\)，若存在某个有限正常数 \(M\) 使得

\[ \lim\limits_{n\rightarrow \infty}\frac{|x_{n+1}-x_\infty|}{|x_n-x_\infty|^2} < M, \]则称序列 \(\{x_n\}\) 平方收敛, 相比于之前提到的线性收敛和超线性收敛，平方收敛的速度最快。

例2.4 序列 \(x_n = 1 + (\frac{1}{n})^{2^n}\) 线性收敛。

\[ \lim_{n\rightarrow\infty}\frac{|x_{n+1} - x_{\infty}|}{|x_n - x_{\infty}|^2} = \frac{(\frac{1}{n+1})^{2^{n+1}}}{(\frac{1}{n})^{2^{n+1}}} = (\frac{n}{n+1})^{2^{n+1}}\leq 1 \]该序列平方收敛。

2.2.4 案例：二分法的收敛速度

二分法在第 \(n\) 次迭代的误差为 \(|b_n-a_n|\)，其中 \(a_n\) 和 \(b_n\) 分别为第 \(n\) 次迭代得到的区间的左右断点，并且每次迭代之后区间的长度减小一半，因此第 \(n\) 次的误差大约为 \(2^{-n}|b_0-a_0|\)，

\[ \frac{|x_{n+1} - x_{\infty}|}{|x_n - x_{\infty}|} = \frac{2^{-(n+1)}|b_0-a_0|}{2^{-n}|b_0-a_0|} = \frac{1}{2}, \]因此二分法线性收敛。

2.3 牛顿法

据记载，巴比伦法则（Babylonian rule，公元前1800-1600 年）已经被用于将平方根近似转换为现代符号，其公式与本书介绍的“牛顿法”相同。 Heron在Metrica一书中（公元50年）描述了相同的计算法则，在较早的书籍中将其称之为为“Heron方法”。12世纪的代数学家Sharaf al-Din al-Tusi给出在数学上等同于牛顿法的方法，而15世纪的阿拉伯数学家Al-Kashi进一步使用了该形式用以寻找根。在西欧，亨利·布里格斯（Henry Briggs）在1633年出版的《不列颠三角学》（Trigonometria Britannica）一书中使用了类似的方法，他采用了一种更为繁琐的方法来求多项式方程式的根。范·舒滕（van Schooten）于1646年出版了该方法的简化版本，由奥格特雷德（Oughtred）在《克拉维斯数学》（Clavis Mathematica）（1647）中复现，尽管当时牛顿似乎并未意识到这一点。这大概是就是牛顿方法的出处。

有关这一历史的详细说明，可在牛顿未出版的1664年笔记本中找到。到1669年，他将连续多项式线性化。但是，与之前已经记载的方法相比，几乎没有证据表明牛顿的方法在概念上更加创新。我们现在广为使用的牛顿-拉夫森（Newton-Raphson）方法的前身其实是牛顿首次将这一方法记录并加以讨论。牛顿的贡献体现在将其转化纯代数过程。而且牛顿使用了更一般的方法和符号来使他的想法更广泛地为人们所接受。牛顿的手稿直到1711年才出版，但较早时私下流出了该手稿的副本。拉夫森在1690年进一步简化了该技术，方法是完全消除连续的多项式，并使了迭代方法。该方法已经有些不同于牛顿的方法。但是，直到托马斯·辛普森（Thomas Simpson）撰写的《关于几个好奇和有用的主题的论文》（On SeveralCurious and Useful Subjects）（1740）时，拉夫森的方法才得以被关注。

牛顿法（Newton Method，or Newton-Raphson method）是最常用且高效的求根算法之一。假设函数 \(f(x)\) 可导并一阶导 \(f^{\prime}(x)\) 连续，且 \(x^*\) 为 \(f(x) = 0\) 的根。设 \(x_0\) 是对 \(x^*\) 的一个好的估计，令 \(x^* = x_0 + h\)。因为 \(x^*\) 是\(f(x) = 0\)的根而且 \(h = x^* - x_0\)，所以 \(h\) 描述了 \(x_0\)距离真实根的距离。

因为 \(h\) 很小，我们通过线性逼近可以得到：

\[0 = f(x^*) = f(x_0+h) \approx f(x_0) + h f^{\prime}(x_0),\]

所以除非 \(f^{\prime}(x_0)\) 接近于0，我们得到：

\[h \approx-\frac{f\left(x_{0}\right)}{f^{\prime}\left(x_{0}\right)}.\]

从而，

\[x^*=x_{0}+h \approx x_{0}-\frac{f\left(x_{0}\right)}{f^{\prime}\left(x_{0}\right)},\]

我们可以把这个新的估计 \(x_1\) 做为对 \(x^*\) 更好的估计：

\[x_{1}=x_{0}-\frac{f\left(x_{0}\right)}{f^{\prime}\left(x_{0}\right)}.\]

如果我们继续更新，就可以得到 \(x_2\)：

\[x_{2}=x_{1}-\frac{f\left(x_{1}\right)}{f^{\prime}\left(x_{1}\right)}.\]

按照这种思路继续迭代下去，就是牛顿法求根。牛顿法更一般的写法如下。

牛顿法

  1. 选择初始猜测点 \(x_0\)，设置 \(n = 0\)。

  2. 按照以下迭代过程进行迭代：

\[\begin{equation} x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)}. \end{equation}\]

  1. 计算 \(|f(x_{n+1})|\)。

    1. 如果 \(|f(x_{n+1})| \leq \epsilon\)，停止迭代；
    2. 否则，返回第 2 步。

下面我们来看一下牛顿法更直观的解释。

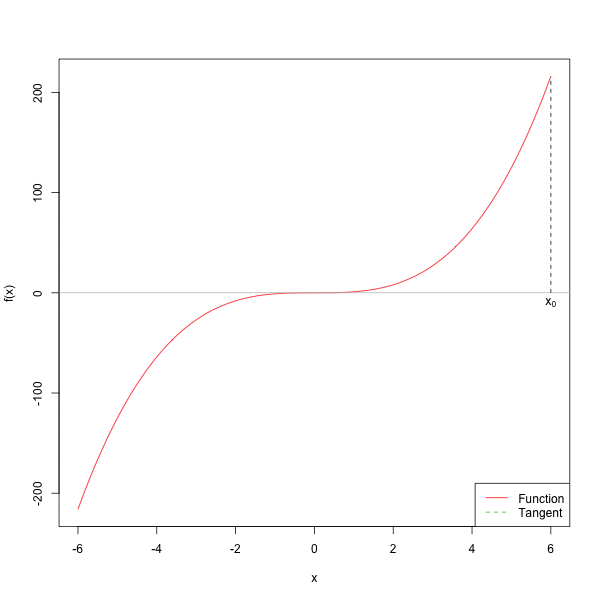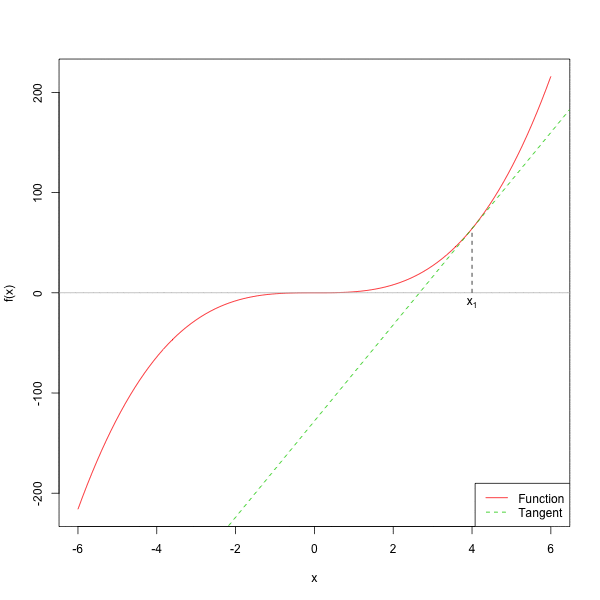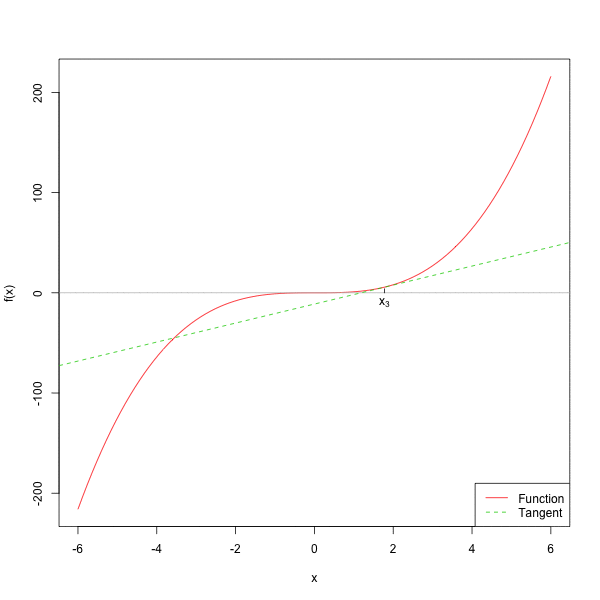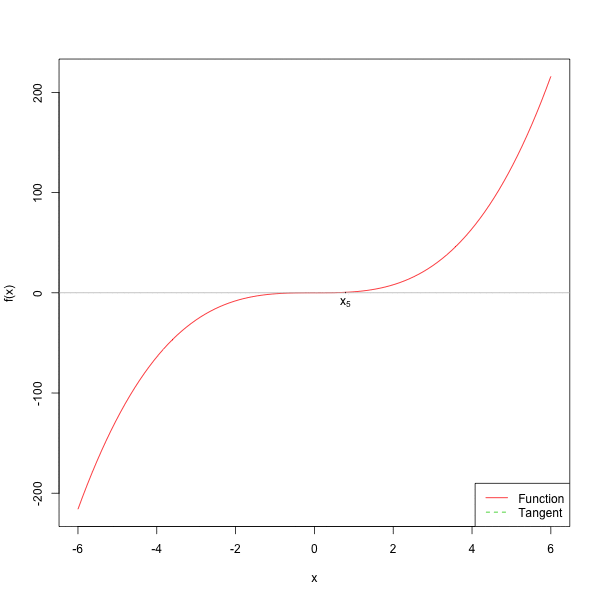
现在我们将牛顿法在 R 中实现，以下 newton.root() 函数中的第一个参数为待求根的函数 \(f(x)\)，因为牛顿法中每一次迭代都需要求 \(f(x)\) 和 \(f^{\prime}(x)\) 在 \(x_n\) 处的取值，因此我们定义了 R 函数 ftn() ，它的输入参数为 \(f(x)\) 的表达式及 \(x\) 的取值，输出为 \(f(x)\) 和 \(f^{\prime}(x)\)。为了以防算法不收敛，我们加入参数 max.iter 来设置最大的迭代次数。具体代码如下。

newton.root <- function(f, x0 = 0, tol = 1e-9,
                        max.iter = 100) {
  x <- x0
  cat(paste0("初始值：x = ", x, "\n"))
  fx <- ftn(f, x)
  iter <-  0
  # xs用来保存每步迭代得到的x值
  xs <- list()
  xs[[iter + 1]] <- x
  # 继续迭代直到满足停止条件
  while ((abs(fx$f) > tol) && (iter < max.iter)) {
    x <- x - fx$f/fx$fgrad
    fx <- ftn(f, x)
    iter <-  iter + 1
    xs[[iter + 1]] <- x
    cat(paste0("迭代第", iter, "次：x = ", x, "\n"))
  }

  # output depends on success of algorithm
  if (abs(fx$f) > tol) {
    cat("算法无法收敛\n")
    return(NULL)
  } else {
    cat("算法收敛\n")
    return(xs)
  }
}

ftn <- function(f, x){
  df <- deriv(f, 'x', func = TRUE)
  dfx <- df(x)
  f <- dfx[1]
  fgrad <- attr(dfx, 'gradient')[1,]
  return(list(f = f, fgrad = fgrad))
}

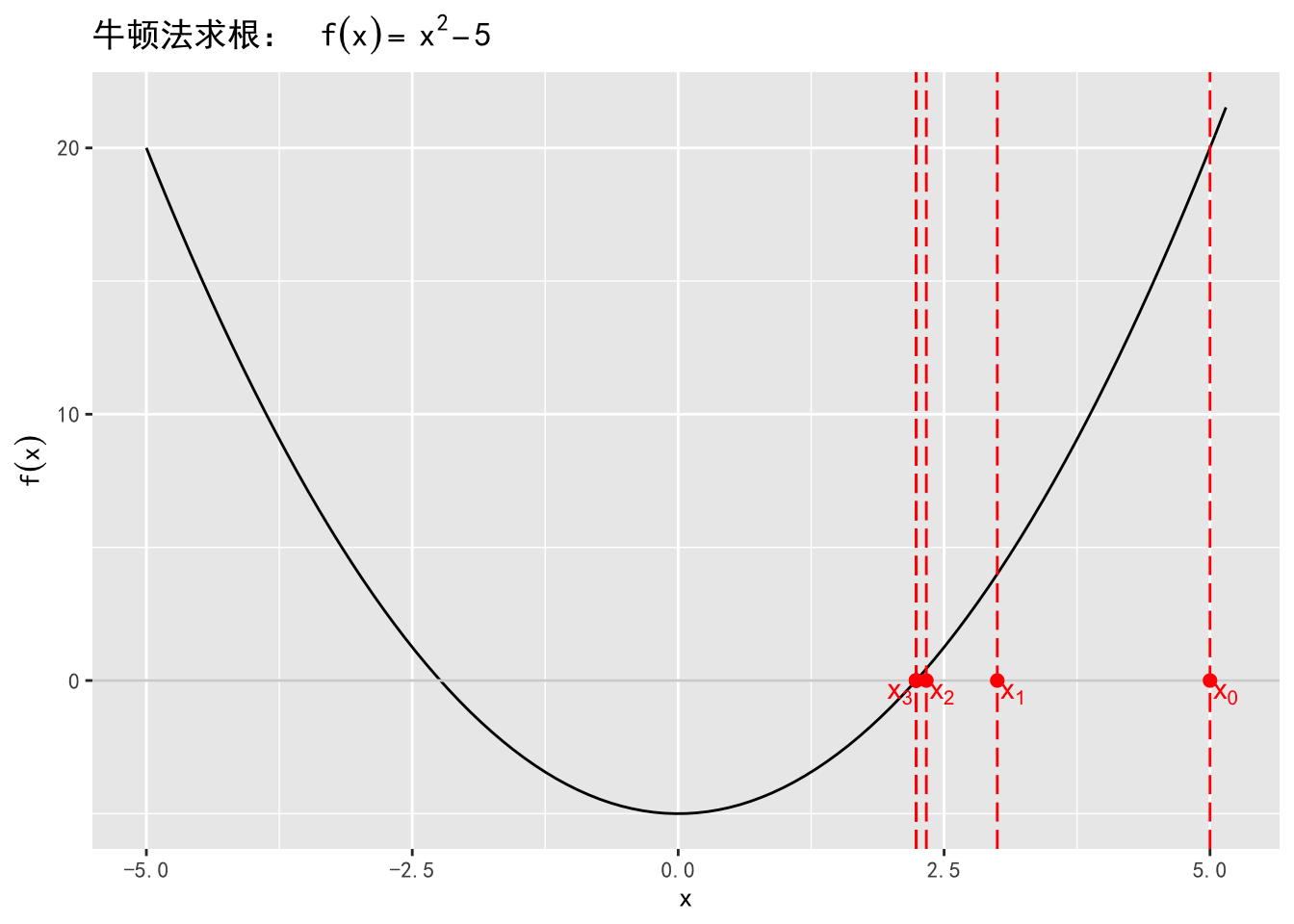
例2.5 求 \(f(x) = x^2 - 5\) 的根。

f <- expression(x^2 - 5)
roots <- unlist(newton.root(f, 5))
#> 初始值：x = 5
#> 迭代第1次：x = 3
#> 迭代第2次：x = 2.33333333333333
#> 迭代第3次：x = 2.23809523809524
#> 迭代第4次：x = 2.23606889564336
#> 迭代第5次：x = 2.23606797749998
#> 算法收敛